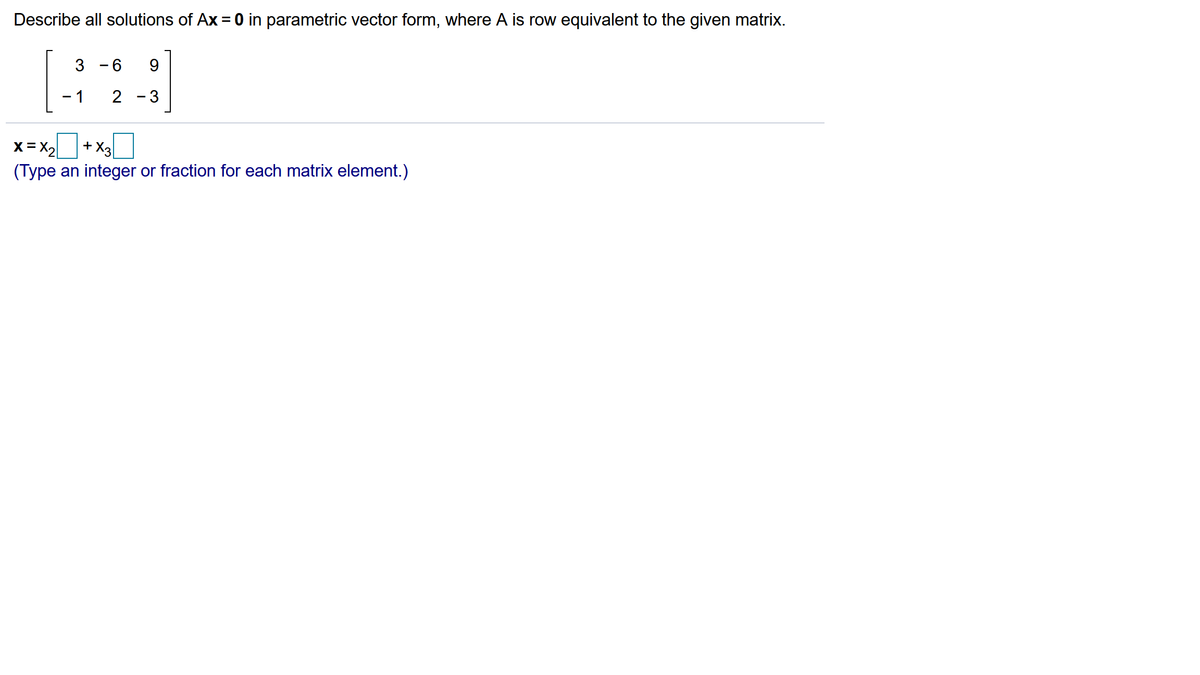
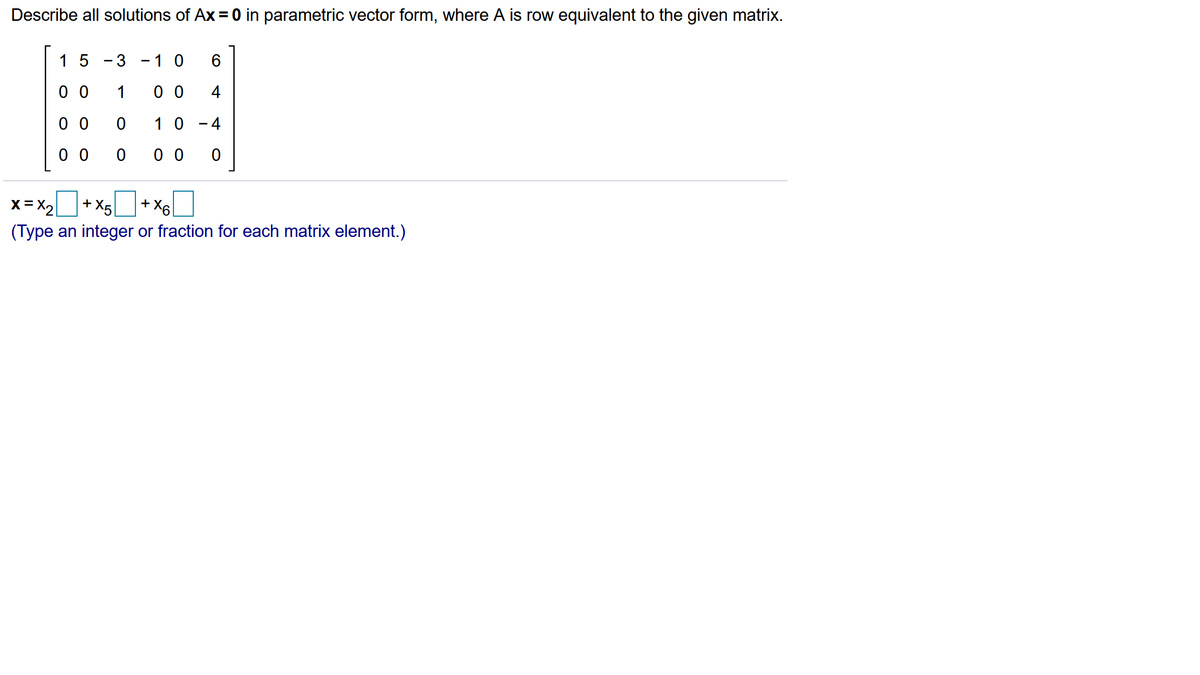
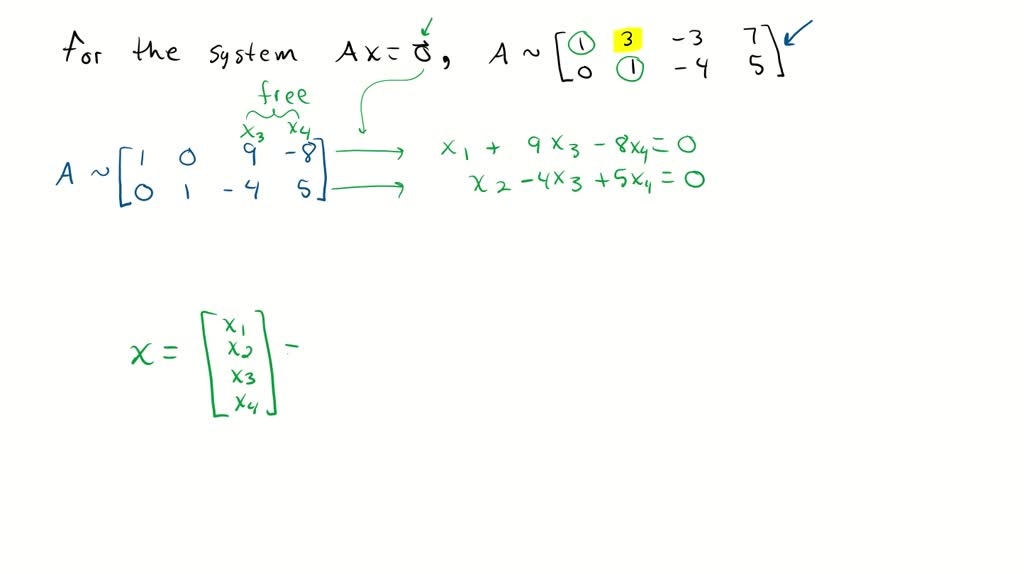Describe All Solutions Of Ax 0 In Parametric Vector Form - Describe all solutions of ax = 0 in parametric vector form, where a is row equivalent to the given matrix. Describe all solutions of $ax=0$ in parametric vector form, where $a$ is row equivalent to the given matrix. X2 x 2 = 0. I need clarification in understanding all solutions of $ax=0$ in parametric vector form where the $a$ is row equivalent to the given. The solutions of ax = 0, where a is row equivalent to the given matrix, can be described in parametric vector form as x = t *. The solution to the equation ax=0 in parametric vector form is a set of vectors where each component of the vector is equal to 0. We can write the general equation, which provides us with a parametric description of the solution set: The given matrix a can be row reduced to find its echelon form.
The solution to the equation ax=0 in parametric vector form is a set of vectors where each component of the vector is equal to 0. We can write the general equation, which provides us with a parametric description of the solution set: Describe all solutions of ax = 0 in parametric vector form, where a is row equivalent to the given matrix. Describe all solutions of $ax=0$ in parametric vector form, where $a$ is row equivalent to the given matrix. X2 x 2 = 0. The solutions of ax = 0, where a is row equivalent to the given matrix, can be described in parametric vector form as x = t *. I need clarification in understanding all solutions of $ax=0$ in parametric vector form where the $a$ is row equivalent to the given. The given matrix a can be row reduced to find its echelon form.
The solutions of ax = 0, where a is row equivalent to the given matrix, can be described in parametric vector form as x = t *. We can write the general equation, which provides us with a parametric description of the solution set: I need clarification in understanding all solutions of $ax=0$ in parametric vector form where the $a$ is row equivalent to the given. The given matrix a can be row reduced to find its echelon form. X2 x 2 = 0. The solution to the equation ax=0 in parametric vector form is a set of vectors where each component of the vector is equal to 0. Describe all solutions of ax = 0 in parametric vector form, where a is row equivalent to the given matrix. Describe all solutions of $ax=0$ in parametric vector form, where $a$ is row equivalent to the given matrix.
Answered Describe all solutions of Ax = 0 in… bartleby
X2 x 2 = 0. The solutions of ax = 0, where a is row equivalent to the given matrix, can be described in parametric vector form as x = t *. I need clarification in understanding all solutions of $ax=0$ in parametric vector form where the $a$ is row equivalent to the given. Describe all solutions of $ax=0$ in.
[Solved] . Describe all solutions of Ax = 0 in parametric vector form
Describe all solutions of $ax=0$ in parametric vector form, where $a$ is row equivalent to the given matrix. The solution to the equation ax=0 in parametric vector form is a set of vectors where each component of the vector is equal to 0. Describe all solutions of ax = 0 in parametric vector form, where a is row equivalent to.
[Solved] Describe all solutions of Ax = 0 in parametric vector form
Describe all solutions of $ax=0$ in parametric vector form, where $a$ is row equivalent to the given matrix. X2 x 2 = 0. The solutions of ax = 0, where a is row equivalent to the given matrix, can be described in parametric vector form as x = t *. We can write the general equation, which provides us with.
Solved 7. Describe all solutions for Ax=0 in parametric vector form
The given matrix a can be row reduced to find its echelon form. The solution to the equation ax=0 in parametric vector form is a set of vectors where each component of the vector is equal to 0. X2 x 2 = 0. The solutions of ax = 0, where a is row equivalent to the given matrix, can be.
SOLVEDDescribe all solutions of Ax = 0 in parametric vector form
X2 x 2 = 0. Describe all solutions of $ax=0$ in parametric vector form, where $a$ is row equivalent to the given matrix. Describe all solutions of ax = 0 in parametric vector form, where a is row equivalent to the given matrix. I need clarification in understanding all solutions of $ax=0$ in parametric vector form where the $a$ is.
SOLVED Describe all solutions of Ax = 0 in parametric vector form
X2 x 2 = 0. The given matrix a can be row reduced to find its echelon form. The solution to the equation ax=0 in parametric vector form is a set of vectors where each component of the vector is equal to 0. We can write the general equation, which provides us with a parametric description of the solution set:.
Describe all solutions of Ax=0 in parametric Vector Form
X2 x 2 = 0. The solution to the equation ax=0 in parametric vector form is a set of vectors where each component of the vector is equal to 0. Describe all solutions of $ax=0$ in parametric vector form, where $a$ is row equivalent to the given matrix. I need clarification in understanding all solutions of $ax=0$ in parametric vector.
SOLVED Describe all solutions of Ax = 0 in parametric vector form
The solution to the equation ax=0 in parametric vector form is a set of vectors where each component of the vector is equal to 0. The given matrix a can be row reduced to find its echelon form. I need clarification in understanding all solutions of $ax=0$ in parametric vector form where the $a$ is row equivalent to the given..
[Solved] Describe all solutions of Ax = 0 in parametric vector form
The solution to the equation ax=0 in parametric vector form is a set of vectors where each component of the vector is equal to 0. I need clarification in understanding all solutions of $ax=0$ in parametric vector form where the $a$ is row equivalent to the given. The given matrix a can be row reduced to find its echelon form..
Answered Describe all solutions of Ax = 0 in… bartleby
The given matrix a can be row reduced to find its echelon form. The solution to the equation ax=0 in parametric vector form is a set of vectors where each component of the vector is equal to 0. I need clarification in understanding all solutions of $ax=0$ in parametric vector form where the $a$ is row equivalent to the given..
We Can Write The General Equation, Which Provides Us With A Parametric Description Of The Solution Set:
The solutions of ax = 0, where a is row equivalent to the given matrix, can be described in parametric vector form as x = t *. The solution to the equation ax=0 in parametric vector form is a set of vectors where each component of the vector is equal to 0. X2 x 2 = 0. The given matrix a can be row reduced to find its echelon form.
Describe All Solutions Of $Ax=0$ In Parametric Vector Form, Where $A$ Is Row Equivalent To The Given Matrix.
I need clarification in understanding all solutions of $ax=0$ in parametric vector form where the $a$ is row equivalent to the given. Describe all solutions of ax = 0 in parametric vector form, where a is row equivalent to the given matrix.