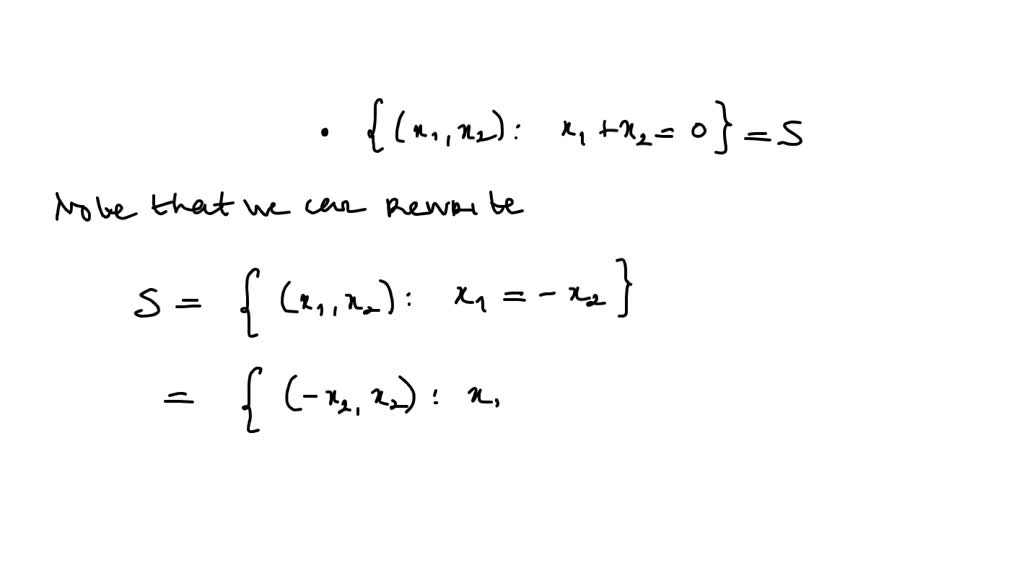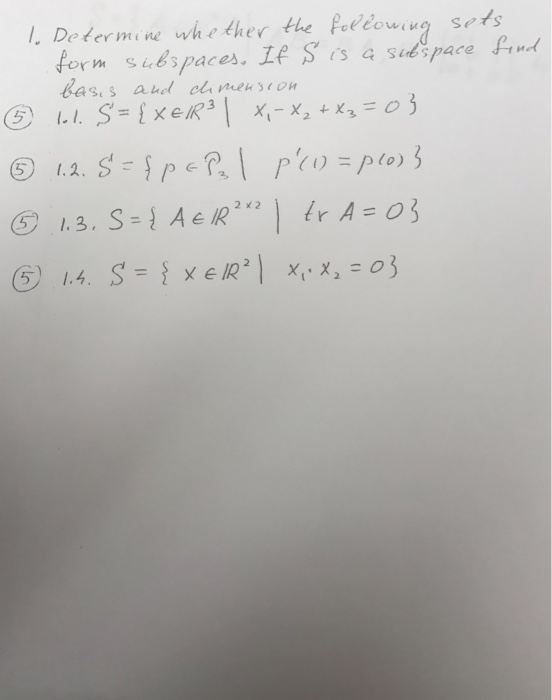Determine Whether The Following Sets Form Subspaces Of R2 - X 1 + x 2 = 0} checking for the line. Determine whether the following sets form subspaces of r2×r2. In mathematics, we can determine whether a set of matrices can serve as subspaces of r2×2 through examining if they satisfy. To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: −> subspaces of r2×r2 b. To determine whether the given sets form subspaces of r², each set must be tested for closure under addition and scalar. The set of all 2×2 diagonal matrices. The task is to identify that the given subsets are the subspaces of r 2 or not (a) a = {(x 1, x 2):
To determine whether the given sets form subspaces of r², each set must be tested for closure under addition and scalar. −> subspaces of r2×r2 b. The task is to identify that the given subsets are the subspaces of r 2 or not (a) a = {(x 1, x 2): To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: In mathematics, we can determine whether a set of matrices can serve as subspaces of r2×2 through examining if they satisfy. Determine whether the following sets form subspaces of r2×r2. The set of all 2×2 diagonal matrices. X 1 + x 2 = 0} checking for the line.
−> subspaces of r2×r2 b. The task is to identify that the given subsets are the subspaces of r 2 or not (a) a = {(x 1, x 2): In mathematics, we can determine whether a set of matrices can serve as subspaces of r2×2 through examining if they satisfy. The set of all 2×2 diagonal matrices. To determine whether the given sets form subspaces of r², each set must be tested for closure under addition and scalar. To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: X 1 + x 2 = 0} checking for the line. Determine whether the following sets form subspaces of r2×r2.
[Solved] Determine whether the following sets form subspaces of R2. (a
The set of all 2×2 diagonal matrices. To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: The task is to identify that the given subsets are the subspaces of r 2 or not (a) a = {(x 1, x 2): To determine whether the given sets form subspaces of r²,.
Solved 4. (15 points) Determine whether the following sets
The task is to identify that the given subsets are the subspaces of r 2 or not (a) a = {(x 1, x 2): In mathematics, we can determine whether a set of matrices can serve as subspaces of r2×2 through examining if they satisfy. To determine whether a set forms a subspace of r2, we need to check if.
SOLVED Question 13.Determine whether the following sets form subspaces
To determine whether the given sets form subspaces of r², each set must be tested for closure under addition and scalar. X 1 + x 2 = 0} checking for the line. −> subspaces of r2×r2 b. The set of all 2×2 diagonal matrices. The task is to identify that the given subsets are the subspaces of r 2 or.
Solved Determine whether the following sets form subspaces.
The task is to identify that the given subsets are the subspaces of r 2 or not (a) a = {(x 1, x 2): In mathematics, we can determine whether a set of matrices can serve as subspaces of r2×2 through examining if they satisfy. To determine whether a set forms a subspace of r2, we need to check if.
SOLVED 1. Determine whether the following sets form subspaces of R? a
The set of all 2×2 diagonal matrices. −> subspaces of r2×r2 b. Determine whether the following sets form subspaces of r2×r2. The task is to identify that the given subsets are the subspaces of r 2 or not (a) a = {(x 1, x 2): To determine whether the given sets form subspaces of r², each set must be tested.
[Solved] Determine whether the following sets form subspaces of R2. (a
X 1 + x 2 = 0} checking for the line. −> subspaces of r2×r2 b. To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: To determine whether the given sets form subspaces of r², each set must be tested for closure under addition and scalar. In mathematics, we can.
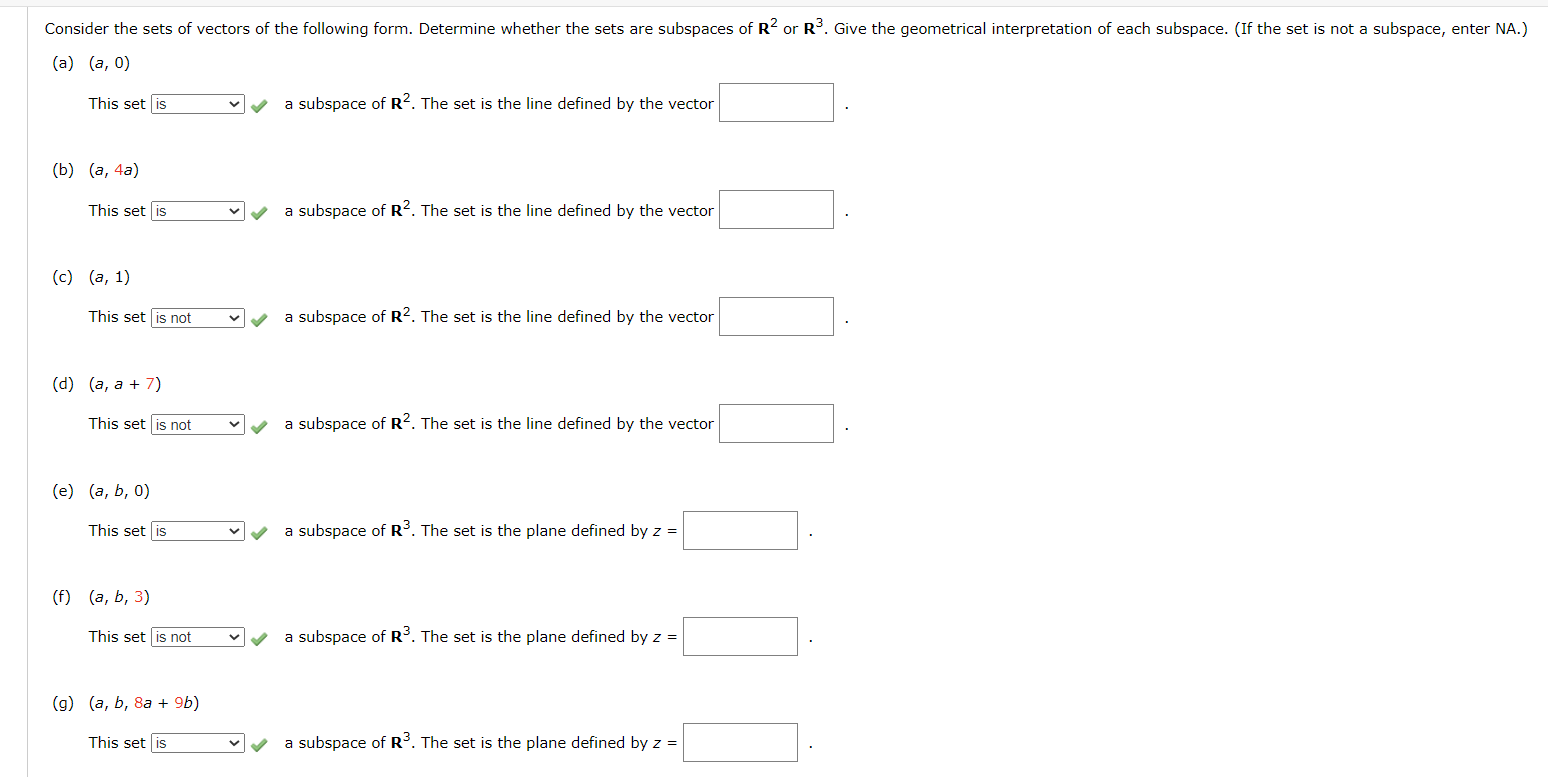
Solved Consider the sets of vectors of the following form.
The set of all 2×2 diagonal matrices. To determine whether the given sets form subspaces of r², each set must be tested for closure under addition and scalar. The task is to identify that the given subsets are the subspaces of r 2 or not (a) a = {(x 1, x 2): In mathematics, we can determine whether a set.
[Solved] Determine whether the following sets form subspaces of R2. (a
To determine whether the given sets form subspaces of r², each set must be tested for closure under addition and scalar. In mathematics, we can determine whether a set of matrices can serve as subspaces of r2×2 through examining if they satisfy. The task is to identify that the given subsets are the subspaces of r 2 or not (a).
Solved Consider the sets of vectors of the following form.
In mathematics, we can determine whether a set of matrices can serve as subspaces of r2×2 through examining if they satisfy. The set of all 2×2 diagonal matrices. X 1 + x 2 = 0} checking for the line. Determine whether the following sets form subspaces of r2×r2. To determine whether the given sets form subspaces of r², each set.
Solved Consider the sets of vectors of the following form.
To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: To determine whether the given sets form subspaces of r², each set must be tested for closure under addition and scalar. Determine whether the following sets form subspaces of r2×r2. The set of all 2×2 diagonal matrices. X 1 + x.
The Task Is To Identify That The Given Subsets Are The Subspaces Of R 2 Or Not (A) A = {(X 1, X 2):
In mathematics, we can determine whether a set of matrices can serve as subspaces of r2×2 through examining if they satisfy. To determine whether the given sets form subspaces of r², each set must be tested for closure under addition and scalar. X 1 + x 2 = 0} checking for the line. The set of all 2×2 diagonal matrices.
Determine Whether The Following Sets Form Subspaces Of R2×R2.
To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: −> subspaces of r2×r2 b.