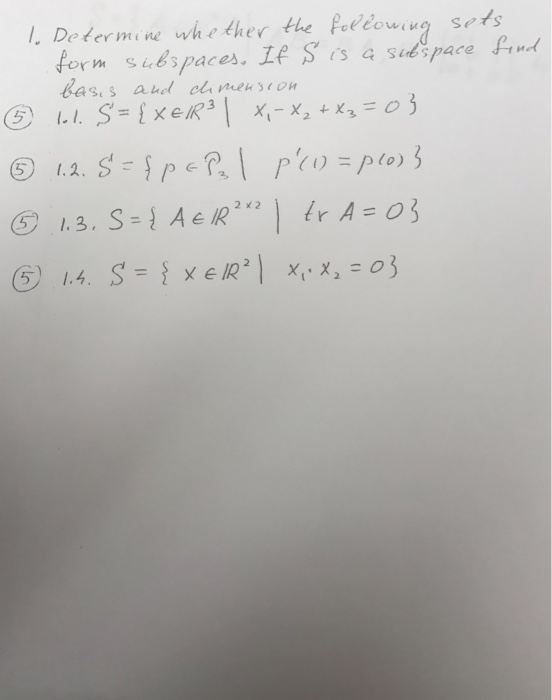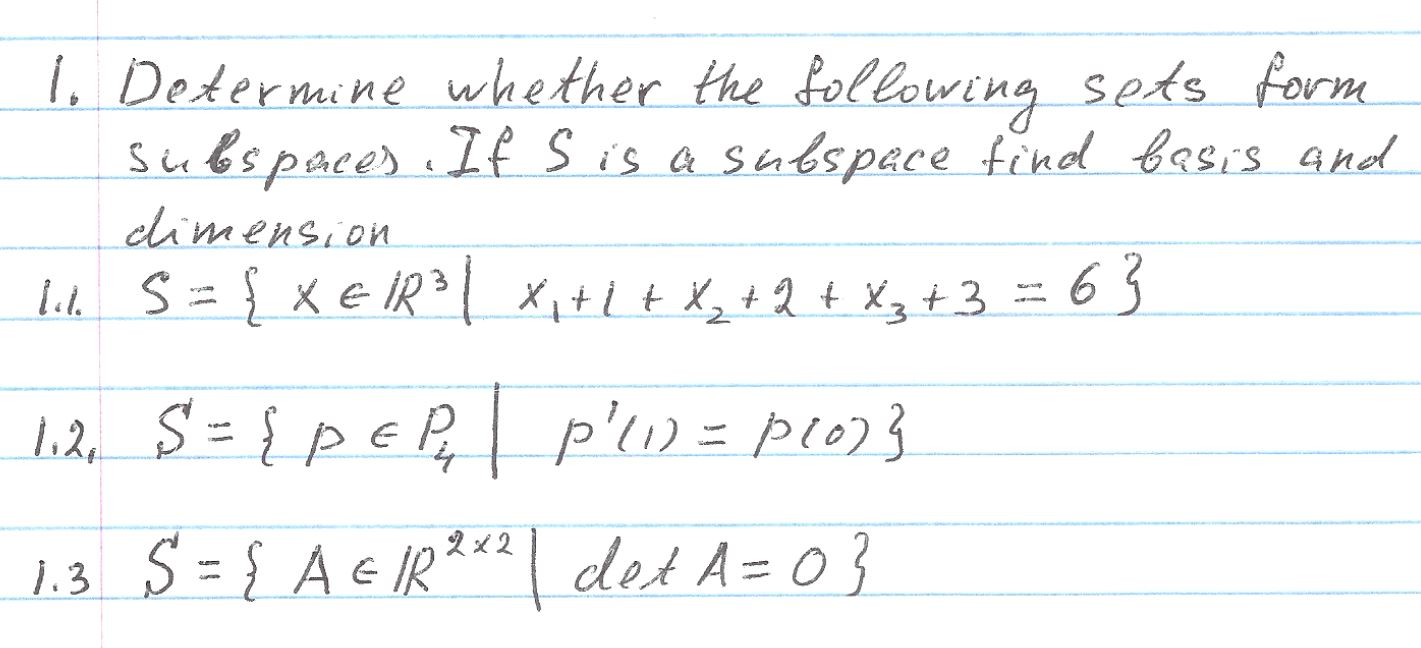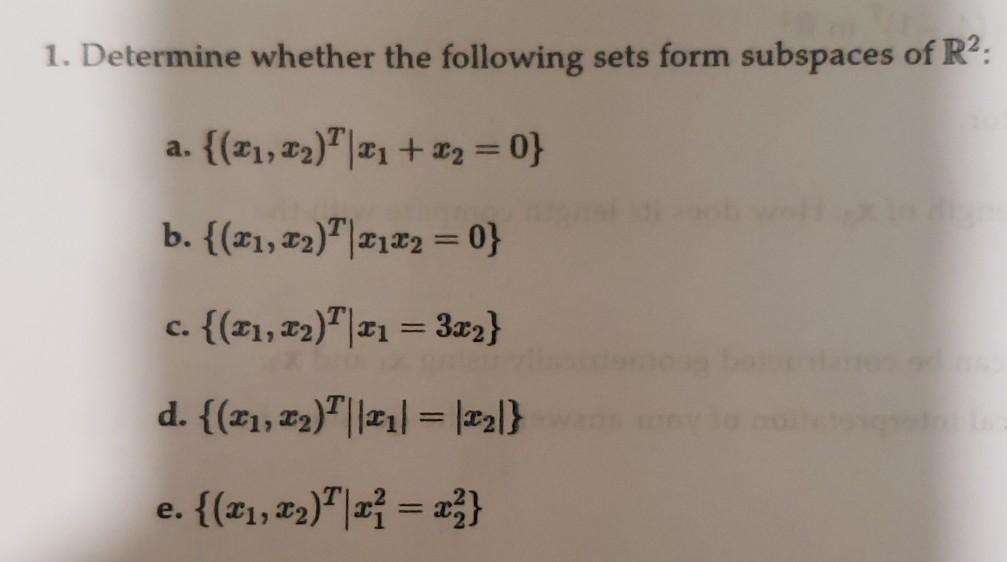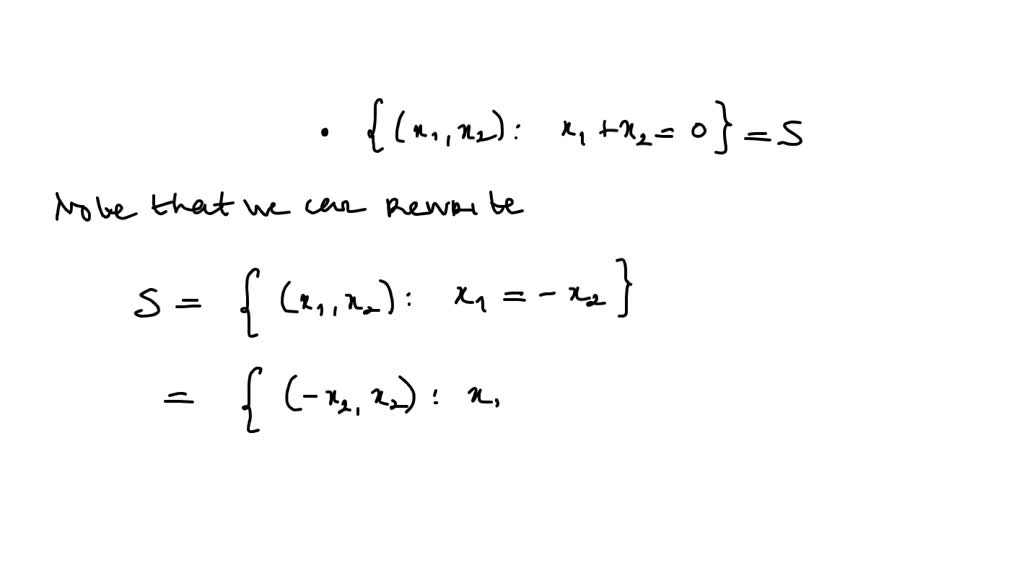Determine Whether The Following Sets Form Subspaces Of - The task is to identify that the given subsets are the subspaces of r 2 or not (a) a = {(x 1, x 2): Determine whether $v:=\{x_1,x_2,x_3\in\mathbb{r}^3|2x_1+5x_2=x_3 \}$ is a subspace of $\mathbb{r}^3$ Check if the zero vector is in set s, by verifying that if x 1 = x 2 = x 3 = 0, then (0,0,0) is an element of s, thus. To determine if a set of vectors is a subspace, checking these properties is crucial. There are 3 steps to solve this one. Without fulfilling even one of them, the set cannot be. Given we have a set $w=\{ (x,y,z) \in \mathbb{r}^3 \;:\; The set of all 2×2 diagonal matrices. Determine whether the following sets form subspaces of r2×r2. X 1 + x 2 = 0} checking for the line.
Given we have a set $w=\{ (x,y,z) \in \mathbb{r}^3 \;:\; To determine if a set of vectors is a subspace, checking these properties is crucial. The set of all 2×2 diagonal matrices. Without fulfilling even one of them, the set cannot be. X 1 + x 2 = 0} checking for the line. Determine whether the following sets form subspaces of r2×r2. −> subspaces of r2×r2 b. Check if the zero vector is in set s, by verifying that if x 1 = x 2 = x 3 = 0, then (0,0,0) is an element of s, thus. Determine whether $v:=\{x_1,x_2,x_3\in\mathbb{r}^3|2x_1+5x_2=x_3 \}$ is a subspace of $\mathbb{r}^3$ To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria:
To determine if a set of vectors is a subspace, checking these properties is crucial. The set of all 2×2 diagonal matrices. The task is to identify that the given subsets are the subspaces of r 2 or not (a) a = {(x 1, x 2): To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: X 1 + x 2 = 0} checking for the line. −> subspaces of r2×r2 b. There are 3 steps to solve this one. Determine whether $v:=\{x_1,x_2,x_3\in\mathbb{r}^3|2x_1+5x_2=x_3 \}$ is a subspace of $\mathbb{r}^3$ Determine whether the following sets form subspaces of r2×r2. Given we have a set $w=\{ (x,y,z) \in \mathbb{r}^3 \;:\;
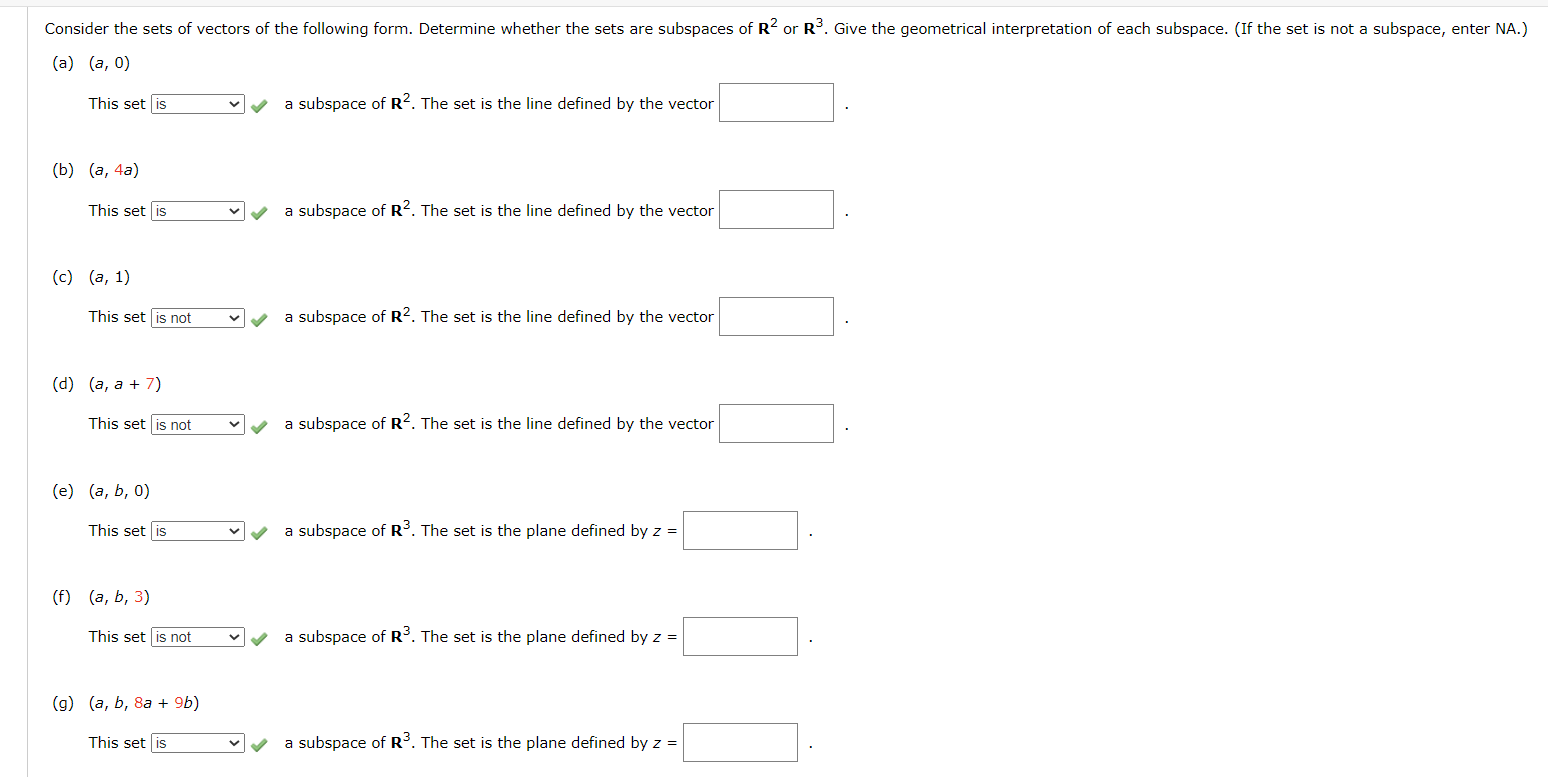
Solved Consider the sets of vectors of the following form.
X 1 + x 2 = 0} checking for the line. There are 3 steps to solve this one. The set of all 2×2 diagonal matrices. To determine if a set of vectors is a subspace, checking these properties is crucial. Check if the zero vector is in set s, by verifying that if x 1 = x 2 =.
Solved Determine whether the following sets form subspaces.
The set of all 2×2 diagonal matrices. Check if the zero vector is in set s, by verifying that if x 1 = x 2 = x 3 = 0, then (0,0,0) is an element of s, thus. Determine whether the following sets form subspaces of r2×r2. Determine whether $v:=\{x_1,x_2,x_3\in\mathbb{r}^3|2x_1+5x_2=x_3 \}$ is a subspace of $\mathbb{r}^3$ X 1 + x.
Solved 1. Determine whether the following sets form
There are 3 steps to solve this one. To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: To determine if a set of vectors is a subspace, checking these properties is crucial. The task is to identify that the given subsets are the subspaces of r 2 or not (a).
Solved 4. (15 points) Determine whether the following sets
Determine whether $v:=\{x_1,x_2,x_3\in\mathbb{r}^3|2x_1+5x_2=x_3 \}$ is a subspace of $\mathbb{r}^3$ X 1 + x 2 = 0} checking for the line. −> subspaces of r2×r2 b. Without fulfilling even one of them, the set cannot be. Check if the zero vector is in set s, by verifying that if x 1 = x 2 = x 3 = 0, then (0,0,0).
Solved Consider the sets of vectors of the following form.
To determine if a set of vectors is a subspace, checking these properties is crucial. −> subspaces of r2×r2 b. X 1 + x 2 = 0} checking for the line. Determine whether the following sets form subspaces of r2×r2. There are 3 steps to solve this one.
⏩SOLVEDDetermine whether the following sets form subspaces of ℝ^3
To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: Determine whether $v:=\{x_1,x_2,x_3\in\mathbb{r}^3|2x_1+5x_2=x_3 \}$ is a subspace of $\mathbb{r}^3$ The task is to identify that the given subsets are the subspaces of r 2 or not (a) a = {(x 1, x 2): −> subspaces of r2×r2 b. X 1 +.
Solved Consider the sets of vectors of the following form.
Given we have a set $w=\{ (x,y,z) \in \mathbb{r}^3 \;:\; −> subspaces of r2×r2 b. Determine whether the following sets form subspaces of r2×r2. Check if the zero vector is in set s, by verifying that if x 1 = x 2 = x 3 = 0, then (0,0,0) is an element of s, thus. Determine whether $v:=\{x_1,x_2,x_3\in\mathbb{r}^3|2x_1+5x_2=x_3 \}$ is.
Solved 5. Determine whether the following sets form
To determine if a set of vectors is a subspace, checking these properties is crucial. To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: Without fulfilling even one of them, the set cannot be. Check if the zero vector is in set s, by verifying that if x 1 =.
Solved 1. Determine whether the following sets form
The set of all 2×2 diagonal matrices. To determine if a set of vectors is a subspace, checking these properties is crucial. Determine whether $v:=\{x_1,x_2,x_3\in\mathbb{r}^3|2x_1+5x_2=x_3 \}$ is a subspace of $\mathbb{r}^3$ X 1 + x 2 = 0} checking for the line. The task is to identify that the given subsets are the subspaces of r 2 or not (a).
SOLVED Question 13.Determine whether the following sets form subspaces
There are 3 steps to solve this one. Check if the zero vector is in set s, by verifying that if x 1 = x 2 = x 3 = 0, then (0,0,0) is an element of s, thus. To determine if a set of vectors is a subspace, checking these properties is crucial. Determine whether the following sets form.
The Task Is To Identify That The Given Subsets Are The Subspaces Of R 2 Or Not (A) A = {(X 1, X 2):
−> subspaces of r2×r2 b. Without fulfilling even one of them, the set cannot be. The set of all 2×2 diagonal matrices. Determine whether the following sets form subspaces of r2×r2.
X 1 + X 2 = 0} Checking For The Line.
To determine whether a set forms a subspace of r2, we need to check if it satisfies three criteria: Check if the zero vector is in set s, by verifying that if x 1 = x 2 = x 3 = 0, then (0,0,0) is an element of s, thus. Determine whether $v:=\{x_1,x_2,x_3\in\mathbb{r}^3|2x_1+5x_2=x_3 \}$ is a subspace of $\mathbb{r}^3$ There are 3 steps to solve this one.
Given We Have A Set $W=\{ (X,Y,Z) \In \Mathbb{R}^3 \;:\;
To determine if a set of vectors is a subspace, checking these properties is crucial.