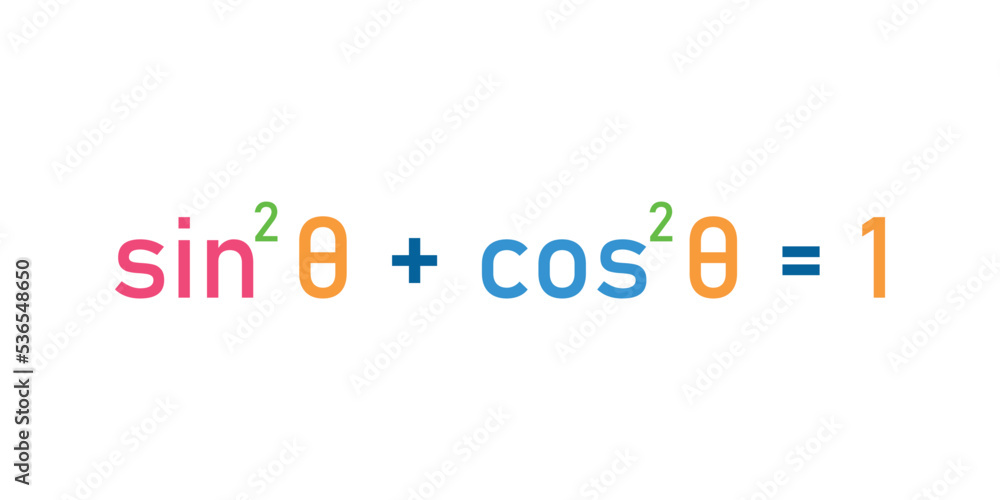Exponential Form Of Sine And Cosine - From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Writing the cosine and sine as the real and imaginary parts of ei , one can easily compute their derivatives from the derivative of the. In euler's formula, if we. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: Similarly, by adding the two equations together, the sines cancel out and after dividing by 2, we get the complex exponential form of the. There is clearly nothing special about the power 2 or cosine alone, so any positive power of sine and cosine can be expanded and then integrated.
Writing the cosine and sine as the real and imaginary parts of ei , one can easily compute their derivatives from the derivative of the. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: There is clearly nothing special about the power 2 or cosine alone, so any positive power of sine and cosine can be expanded and then integrated. In euler's formula, if we. Similarly, by adding the two equations together, the sines cancel out and after dividing by 2, we get the complex exponential form of the.
Writing the cosine and sine as the real and imaginary parts of ei , one can easily compute their derivatives from the derivative of the. There is clearly nothing special about the power 2 or cosine alone, so any positive power of sine and cosine can be expanded and then integrated. Similarly, by adding the two equations together, the sines cancel out and after dividing by 2, we get the complex exponential form of the. In euler's formula, if we. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions:
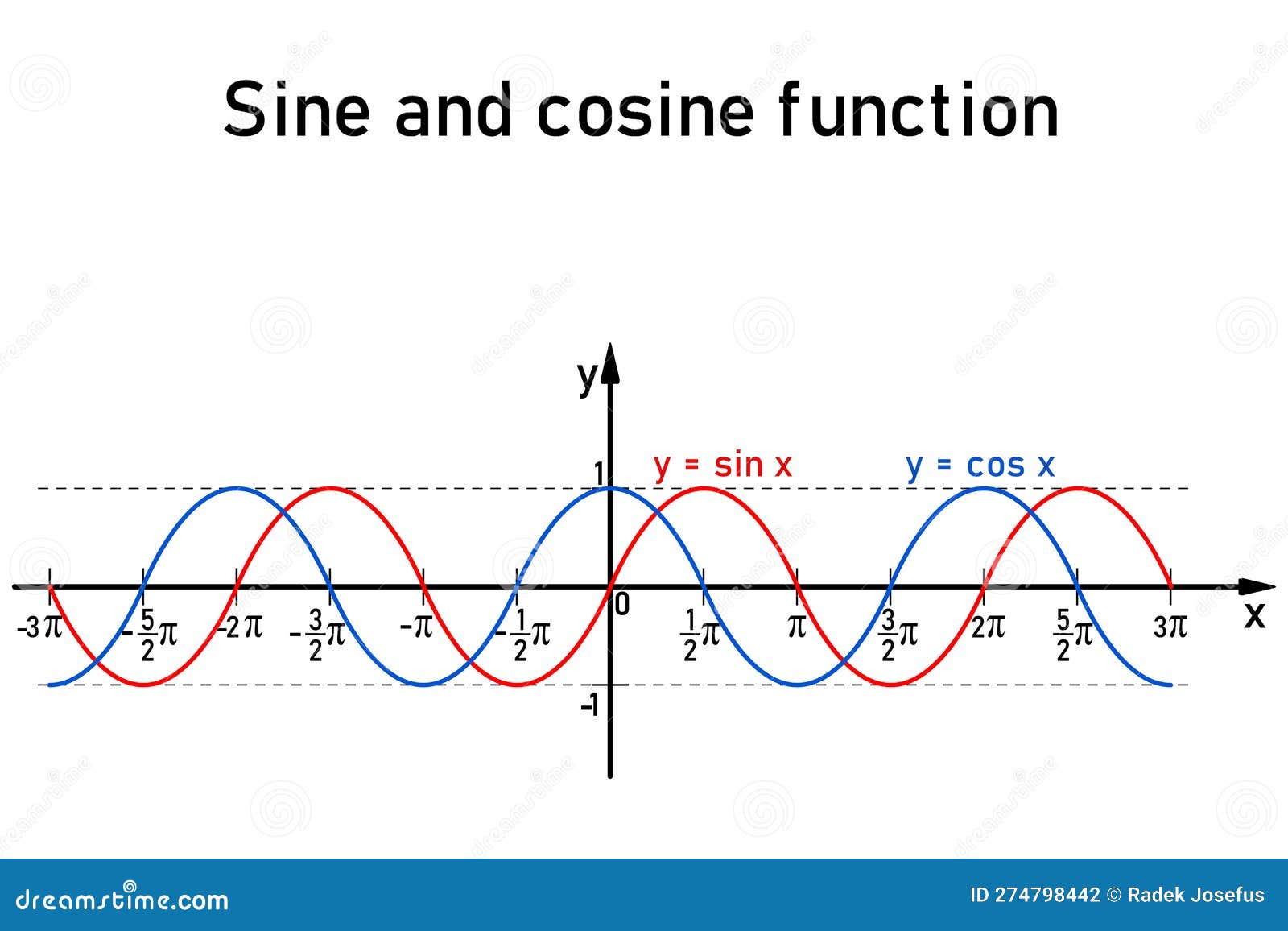
Graphic Representation of the Goniometric Sine and Cosine Functions on
Writing the cosine and sine as the real and imaginary parts of ei , one can easily compute their derivatives from the derivative of the. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: There is.
Drawing On Math Sine and Cosine Waves with Activity Builder
In euler's formula, if we. Writing the cosine and sine as the real and imaginary parts of ei , one can easily compute their derivatives from the derivative of the. Similarly, by adding the two equations together, the sines cancel out and after dividing by 2, we get the complex exponential form of the. From these relations and the properties.
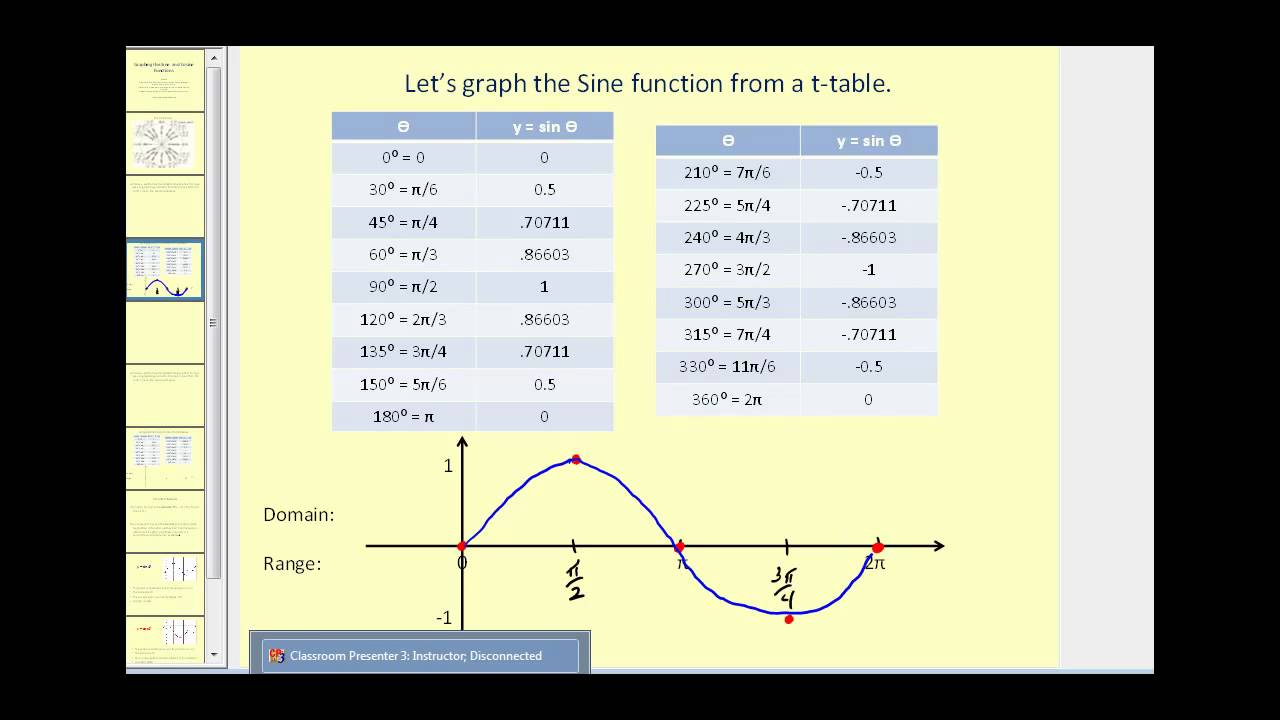
Sine Cosine Table Values Review Home Decor
Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: Writing the cosine and sine as the real and imaginary parts of ei , one can easily compute their derivatives from the derivative of the. There is clearly nothing special about the power 2 or cosine alone, so any positive power of sine and cosine can.
Sine and Cosine Rule Match Up Starting Points Maths
From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Similarly, by adding the two equations together, the sines cancel out and after dividing by 2, we get the complex exponential form of the. In euler's formula, if we. Euler's formula is a relationship between exponents of imaginary numbers and the.
Sine and cosine problems Math Tutoring & Exercises
From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Similarly, by adding the two equations together, the sines cancel out and after dividing by 2, we get the complex exponential form of the. Writing the cosine and sine as the real and imaginary parts of ei , one can easily.
Solved HWP 06.02 Complex exponential and sinecosine
Similarly, by adding the two equations together, the sines cancel out and after dividing by 2, we get the complex exponential form of the. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. There is clearly nothing special about the power 2 or cosine alone, so any positive power of.
Sine, cosine and exponential integrals The Mathematical Gazette
From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Similarly, by adding the two equations together, the sines cancel out and after dividing by 2, we get the complex exponential form of the. In euler's formula, if we. There is clearly nothing special about the power 2 or cosine alone,.
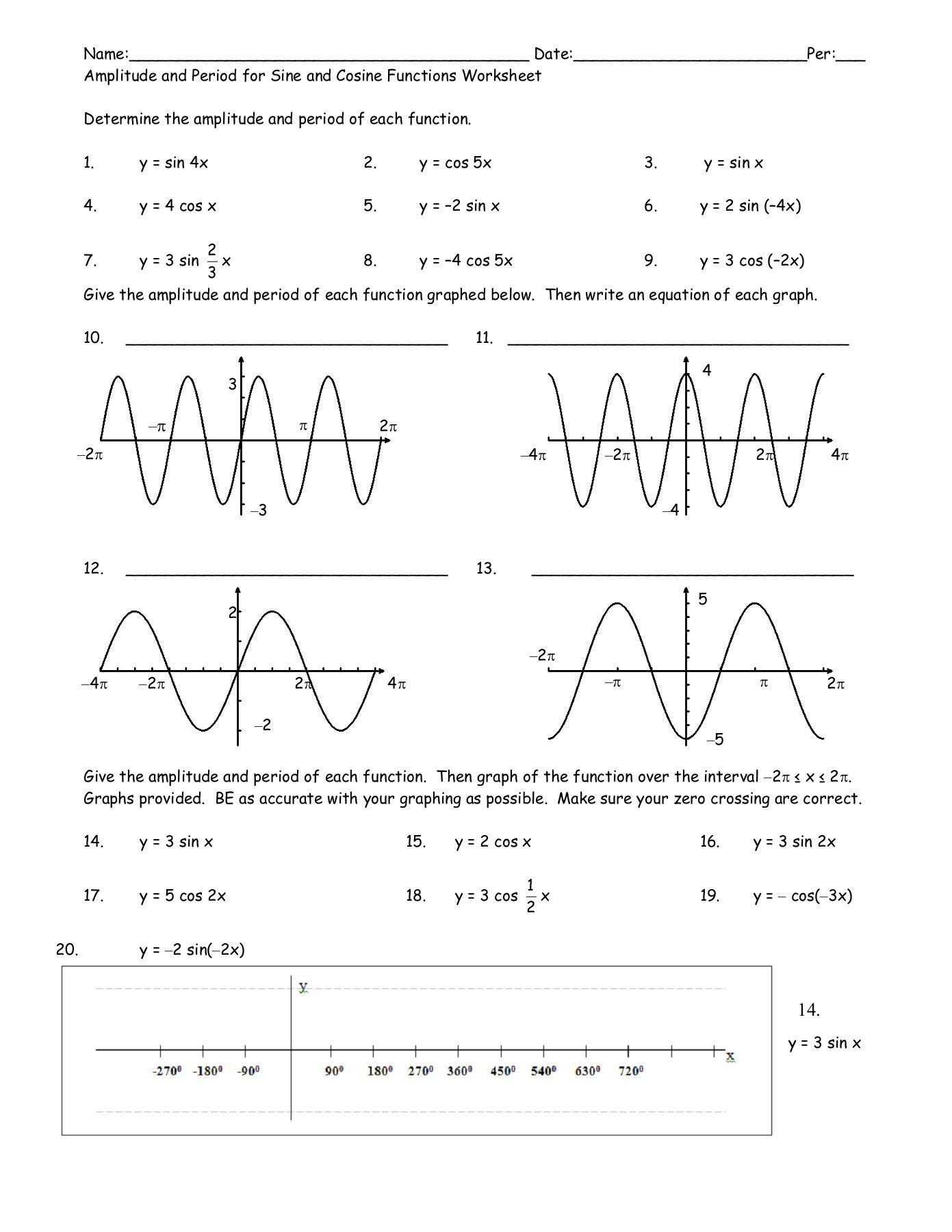
Pictures Graphing Sine And Cosine Worksheet Getadating
From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. There is clearly nothing special about the power 2 or cosine alone, so any positive power of sine and cosine can be expanded and then integrated. Writing the cosine and sine as the real and imaginary parts of ei , one.
pythagorean identities formulas. Sine squared plus cosine squared equal
There is clearly nothing special about the power 2 or cosine alone, so any positive power of sine and cosine can be expanded and then integrated. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. In euler's formula, if we. Writing the cosine and sine as the real and imaginary.
Graphing Sine And Cosine Functions Worksheet Function Worksheets
Similarly, by adding the two equations together, the sines cancel out and after dividing by 2, we get the complex exponential form of the. Writing the cosine and sine as the real and imaginary parts of ei , one can easily compute their derivatives from the derivative of the. In euler's formula, if we. There is clearly nothing special about.
Similarly, By Adding The Two Equations Together, The Sines Cancel Out And After Dividing By 2, We Get The Complex Exponential Form Of The.
In euler's formula, if we. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: There is clearly nothing special about the power 2 or cosine alone, so any positive power of sine and cosine can be expanded and then integrated.