Is The Echelon Form Of A Matrix Unique - Does anybody know how to prove this theorem? The book has no proof showing each matrix is row equivalent to one and only one reduced echelon matrix. Basically the matrix a determines its null space, which in turn equals the graph of a linear transformation whose matrix is the negative of the unknown part of the reduced echelon form. I am wondering how this can possibly be a unique matrix when any nonsingular matrix is row equivalent to the identity matrix,. $\begingroup$ one important addition is that even though the ref is not unique, a lot of the most useful properties are unique, and will not change from ref to ref. Every matrix has a unique reduced row echelon form. Stack exchange network consists of 183 q&a communities including stack overflow, the largest, most trusted online community for developers to learn, share their.
Every matrix has a unique reduced row echelon form. $\begingroup$ one important addition is that even though the ref is not unique, a lot of the most useful properties are unique, and will not change from ref to ref. I am wondering how this can possibly be a unique matrix when any nonsingular matrix is row equivalent to the identity matrix,. Basically the matrix a determines its null space, which in turn equals the graph of a linear transformation whose matrix is the negative of the unknown part of the reduced echelon form. Does anybody know how to prove this theorem? Stack exchange network consists of 183 q&a communities including stack overflow, the largest, most trusted online community for developers to learn, share their. The book has no proof showing each matrix is row equivalent to one and only one reduced echelon matrix.
Every matrix has a unique reduced row echelon form. I am wondering how this can possibly be a unique matrix when any nonsingular matrix is row equivalent to the identity matrix,. $\begingroup$ one important addition is that even though the ref is not unique, a lot of the most useful properties are unique, and will not change from ref to ref. The book has no proof showing each matrix is row equivalent to one and only one reduced echelon matrix. Does anybody know how to prove this theorem? Basically the matrix a determines its null space, which in turn equals the graph of a linear transformation whose matrix is the negative of the unknown part of the reduced echelon form. Stack exchange network consists of 183 q&a communities including stack overflow, the largest, most trusted online community for developers to learn, share their.
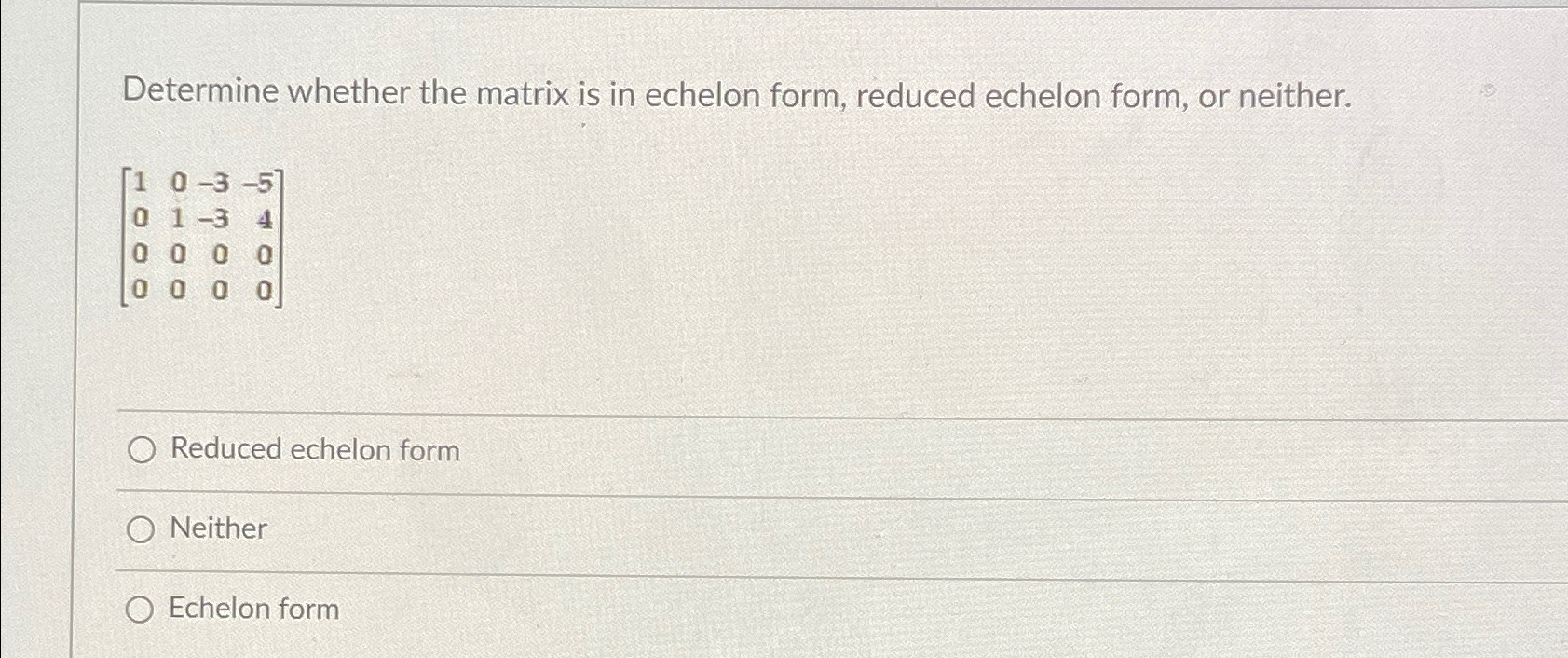
Solved Determine whether the matrix is in echelon form,
Basically the matrix a determines its null space, which in turn equals the graph of a linear transformation whose matrix is the negative of the unknown part of the reduced echelon form. Every matrix has a unique reduced row echelon form. I am wondering how this can possibly be a unique matrix when any nonsingular matrix is row equivalent to.
Solved Is the matrix below in echelon form, reduced echelon
Does anybody know how to prove this theorem? Every matrix has a unique reduced row echelon form. I am wondering how this can possibly be a unique matrix when any nonsingular matrix is row equivalent to the identity matrix,. Stack exchange network consists of 183 q&a communities including stack overflow, the largest, most trusted online community for developers to learn,.
Echelon Form Of A Matrix
The book has no proof showing each matrix is row equivalent to one and only one reduced echelon matrix. Does anybody know how to prove this theorem? $\begingroup$ one important addition is that even though the ref is not unique, a lot of the most useful properties are unique, and will not change from ref to ref. Stack exchange network.
Reduced Echelon Form Matrix
Stack exchange network consists of 183 q&a communities including stack overflow, the largest, most trusted online community for developers to learn, share their. Basically the matrix a determines its null space, which in turn equals the graph of a linear transformation whose matrix is the negative of the unknown part of the reduced echelon form. The book has no proof.
Row Echelon Form Matrix
The book has no proof showing each matrix is row equivalent to one and only one reduced echelon matrix. Basically the matrix a determines its null space, which in turn equals the graph of a linear transformation whose matrix is the negative of the unknown part of the reduced echelon form. I am wondering how this can possibly be a.
Echelon Form
I am wondering how this can possibly be a unique matrix when any nonsingular matrix is row equivalent to the identity matrix,. Every matrix has a unique reduced row echelon form. Does anybody know how to prove this theorem? The book has no proof showing each matrix is row equivalent to one and only one reduced echelon matrix. $\begingroup$ one.
Echelon Form of a Matrix Matrix (Mathematics) Linear Algebra
I am wondering how this can possibly be a unique matrix when any nonsingular matrix is row equivalent to the identity matrix,. Every matrix has a unique reduced row echelon form. Does anybody know how to prove this theorem? Stack exchange network consists of 183 q&a communities including stack overflow, the largest, most trusted online community for developers to learn,.
Row Echelon Form Vs Reduced Row Echelon Form, 57 OFF
Stack exchange network consists of 183 q&a communities including stack overflow, the largest, most trusted online community for developers to learn, share their. Every matrix has a unique reduced row echelon form. Basically the matrix a determines its null space, which in turn equals the graph of a linear transformation whose matrix is the negative of the unknown part of.
What Is Echelon Form Of A Matrix
Does anybody know how to prove this theorem? Every matrix has a unique reduced row echelon form. I am wondering how this can possibly be a unique matrix when any nonsingular matrix is row equivalent to the identity matrix,. The book has no proof showing each matrix is row equivalent to one and only one reduced echelon matrix. $\begingroup$ one.
Echelon Form
Stack exchange network consists of 183 q&a communities including stack overflow, the largest, most trusted online community for developers to learn, share their. The book has no proof showing each matrix is row equivalent to one and only one reduced echelon matrix. Does anybody know how to prove this theorem? Basically the matrix a determines its null space, which in.
Basically The Matrix A Determines Its Null Space, Which In Turn Equals The Graph Of A Linear Transformation Whose Matrix Is The Negative Of The Unknown Part Of The Reduced Echelon Form.
I am wondering how this can possibly be a unique matrix when any nonsingular matrix is row equivalent to the identity matrix,. Every matrix has a unique reduced row echelon form. $\begingroup$ one important addition is that even though the ref is not unique, a lot of the most useful properties are unique, and will not change from ref to ref. Stack exchange network consists of 183 q&a communities including stack overflow, the largest, most trusted online community for developers to learn, share their.
Does Anybody Know How To Prove This Theorem?
The book has no proof showing each matrix is row equivalent to one and only one reduced echelon matrix.