Minterms In Numerical Form - Every boolean function can be. In this section we will introduce two standard forms for boolean functions: The minterm and the maxterm. When a boolean function or logical expression is expressed in the ssop (standard sum of product) form or canonical form, then each term of the. A minterm of n variables = product of n literals in which each variable appears exactly once either in t or f form, but not in both. When expressed either way, it is. Any boolean function can be expressed as a sum of minterms or a product of maxterms;
Any boolean function can be expressed as a sum of minterms or a product of maxterms; The minterm and the maxterm. A minterm of n variables = product of n literals in which each variable appears exactly once either in t or f form, but not in both. In this section we will introduce two standard forms for boolean functions: Every boolean function can be. When a boolean function or logical expression is expressed in the ssop (standard sum of product) form or canonical form, then each term of the. When expressed either way, it is.
When expressed either way, it is. Every boolean function can be. Any boolean function can be expressed as a sum of minterms or a product of maxterms; A minterm of n variables = product of n literals in which each variable appears exactly once either in t or f form, but not in both. The minterm and the maxterm. In this section we will introduce two standard forms for boolean functions: When a boolean function or logical expression is expressed in the ssop (standard sum of product) form or canonical form, then each term of the.
Writing Numbers in Standard, Word, and Expanded Forms ExperTuition
In this section we will introduce two standard forms for boolean functions: Every boolean function can be. When expressed either way, it is. The minterm and the maxterm. Any boolean function can be expressed as a sum of minterms or a product of maxterms;
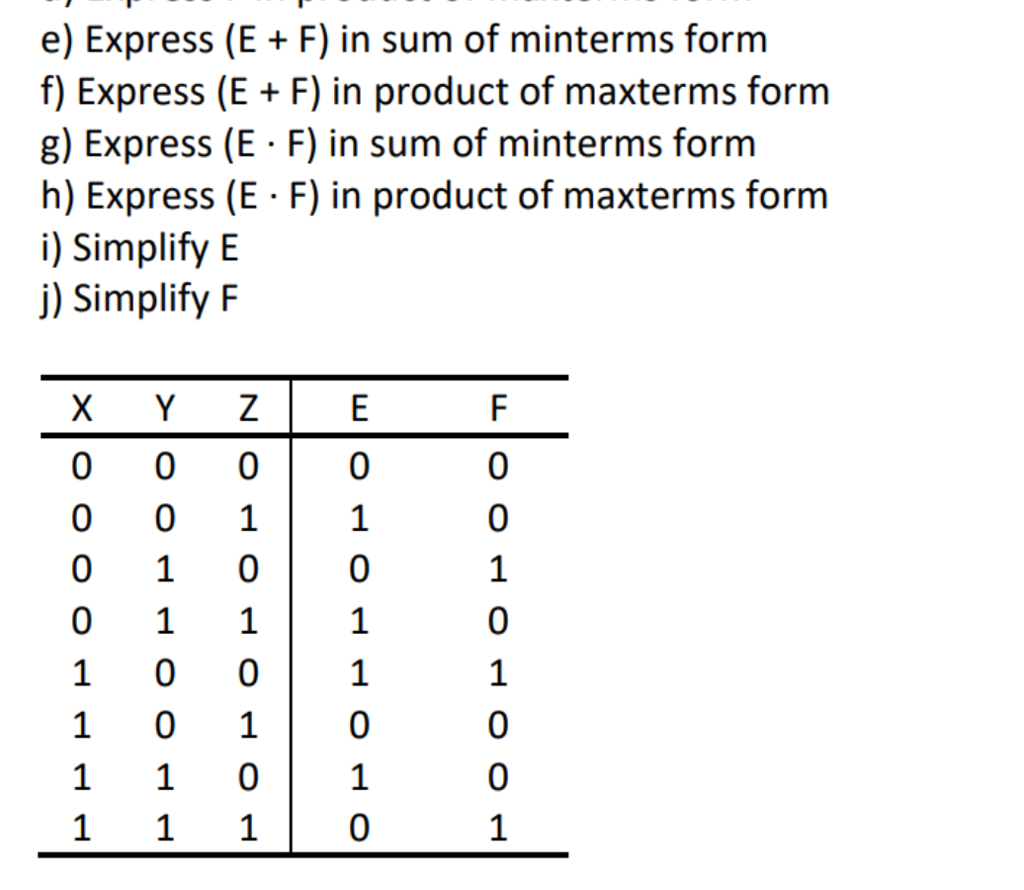
Solved e) Express (E F) in sum of minterms form f) Express
In this section we will introduce two standard forms for boolean functions: Any boolean function can be expressed as a sum of minterms or a product of maxterms; Every boolean function can be. When expressed either way, it is. When a boolean function or logical expression is expressed in the ssop (standard sum of product) form or canonical form, then.
Numerical Expression For Preschoolers Definition & Examples
Every boolean function can be. The minterm and the maxterm. When a boolean function or logical expression is expressed in the ssop (standard sum of product) form or canonical form, then each term of the. A minterm of n variables = product of n literals in which each variable appears exactly once either in t or f form, but not.
Free Evaluate Numerical Expressions Involving Integers Template Edit
When a boolean function or logical expression is expressed in the ssop (standard sum of product) form or canonical form, then each term of the. The minterm and the maxterm. In this section we will introduce two standard forms for boolean functions: Every boolean function can be. Any boolean function can be expressed as a sum of minterms or a.
Numericals Midterm EXAM Numerical Methods Studocu
The minterm and the maxterm. When expressed either way, it is. When a boolean function or logical expression is expressed in the ssop (standard sum of product) form or canonical form, then each term of the. Every boolean function can be. In this section we will introduce two standard forms for boolean functions:
Solved a. Show the minterms in numerical form b. Show an
The minterm and the maxterm. A minterm of n variables = product of n literals in which each variable appears exactly once either in t or f form, but not in both. Any boolean function can be expressed as a sum of minterms or a product of maxterms; In this section we will introduce two standard forms for boolean functions:.
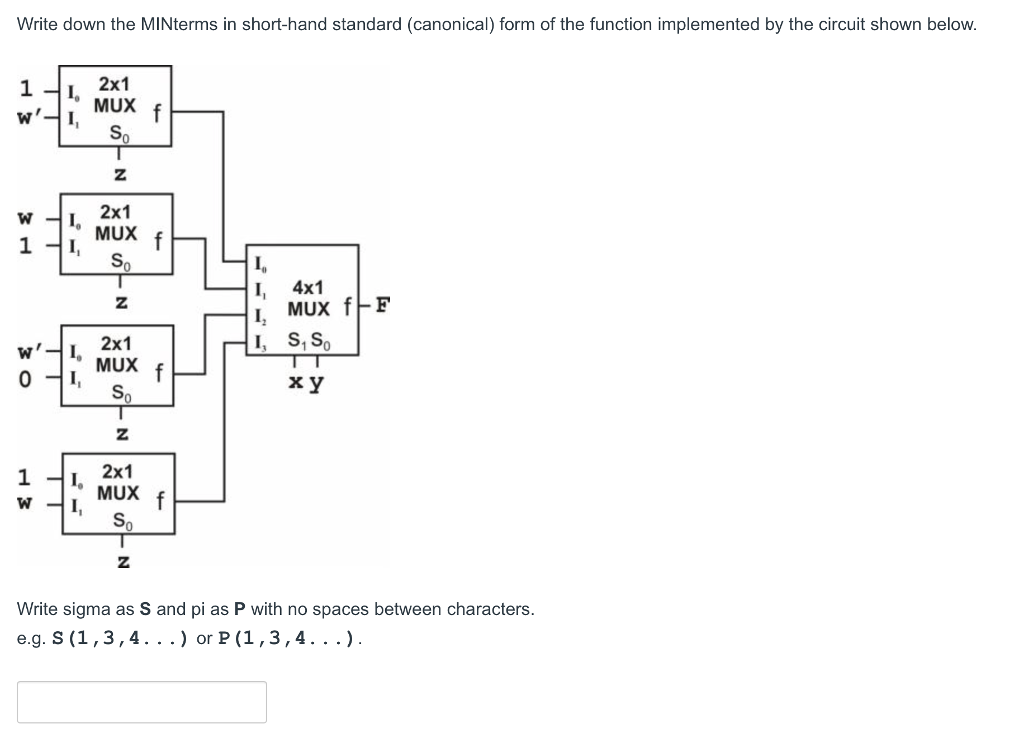
Solved Write down the MINterms in shorthand standard
When a boolean function or logical expression is expressed in the ssop (standard sum of product) form or canonical form, then each term of the. The minterm and the maxterm. Any boolean function can be expressed as a sum of minterms or a product of maxterms; A minterm of n variables = product of n literals in which each variable.
Solved a) Show the minterms in numerical form. b) Show the
A minterm of n variables = product of n literals in which each variable appears exactly once either in t or f form, but not in both. Any boolean function can be expressed as a sum of minterms or a product of maxterms; The minterm and the maxterm. When expressed either way, it is. When a boolean function or logical.
Solved I need all minterms in the form of the equation
A minterm of n variables = product of n literals in which each variable appears exactly once either in t or f form, but not in both. Every boolean function can be. When expressed either way, it is. Any boolean function can be expressed as a sum of minterms or a product of maxterms; The minterm and the maxterm.
Solved 7. (2+2+2+2+2) For the following truth table Function
Every boolean function can be. A minterm of n variables = product of n literals in which each variable appears exactly once either in t or f form, but not in both. In this section we will introduce two standard forms for boolean functions: When expressed either way, it is. The minterm and the maxterm.
Every Boolean Function Can Be.
The minterm and the maxterm. When a boolean function or logical expression is expressed in the ssop (standard sum of product) form or canonical form, then each term of the. A minterm of n variables = product of n literals in which each variable appears exactly once either in t or f form, but not in both. When expressed either way, it is.
In This Section We Will Introduce Two Standard Forms For Boolean Functions:
Any boolean function can be expressed as a sum of minterms or a product of maxterms;