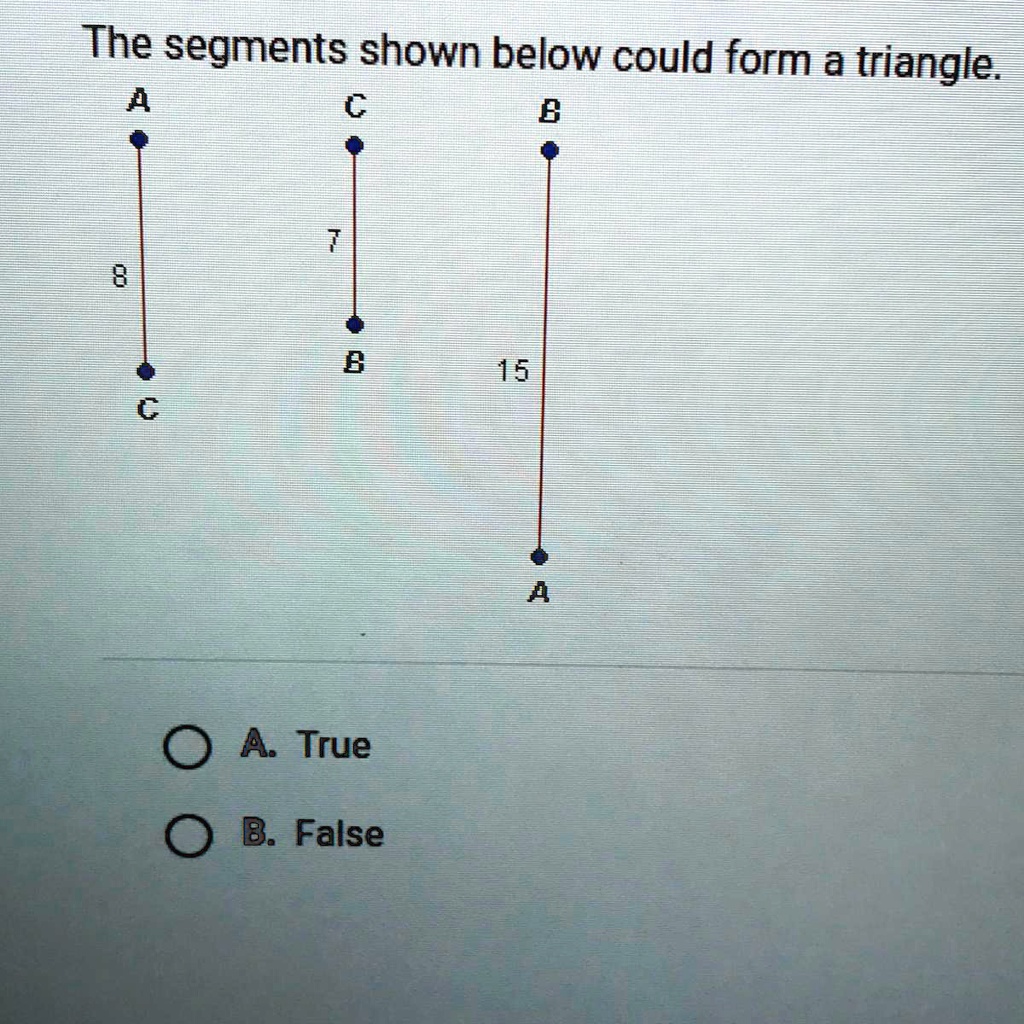
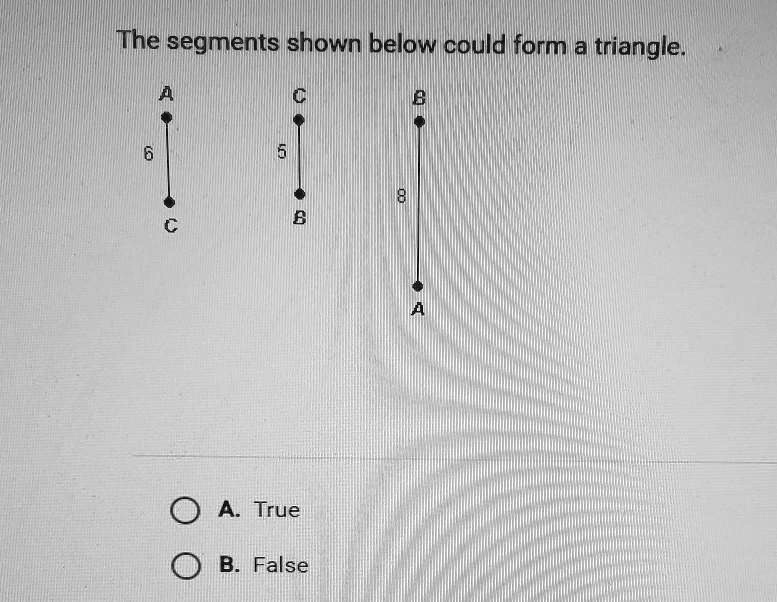
The Segment Shown Below Could Form A Triangle

The Segment Shown Below Could Form A Triangle - According to the triangle inequality theorem, this is a necessary. In euclidean geometry, each and every three points that are not collinear produce a distinct triangle. In order to form a triangle sum of the lengths of any two sides must always be greater than the length of the third side. Here, 6 + 5 = 11 > 8. 1 check if the sum of any two sides of the triangle is greater than the third side. To determine if the segments shown can form a triangle, we can apply the triangle inequality theorem. It's one of the fundamental geometric shapes.

1 check if the sum of any two sides of the triangle is greater than the third side. It's one of the fundamental geometric shapes. According to the triangle inequality theorem, this is a necessary. In order to form a triangle sum of the lengths of any two sides must always be greater than the length of the third side. To determine if the segments shown can form a triangle, we can apply the triangle inequality theorem. Here, 6 + 5 = 11 > 8. In euclidean geometry, each and every three points that are not collinear produce a distinct triangle.

In order to form a triangle sum of the lengths of any two sides must always be greater than the length of the third side. It's one of the fundamental geometric shapes. In euclidean geometry, each and every three points that are not collinear produce a distinct triangle. According to the triangle inequality theorem, this is a necessary. 1 check if the sum of any two sides of the triangle is greater than the third side. To determine if the segments shown can form a triangle, we can apply the triangle inequality theorem. Here, 6 + 5 = 11 > 8.

Solved Question 5 0 The segments shown below could form a triangle. 1

1 check if the sum of any two sides of the triangle is greater than the third side. It's one of the fundamental geometric shapes. Here, 6 + 5 = 11 > 8. To determine if the segments shown can form a triangle, we can apply the triangle inequality theorem. In order to form a triangle sum of the lengths.

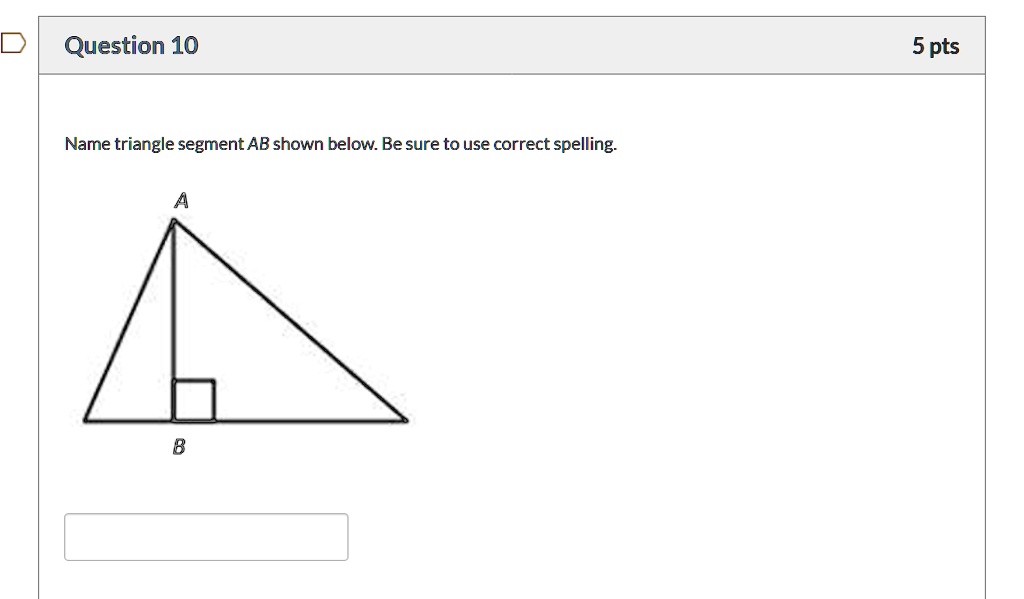
Name the triangle segment AB shown below. Be sure to use correct spelling.

In order to form a triangle sum of the lengths of any two sides must always be greater than the length of the third side. According to the triangle inequality theorem, this is a necessary. To determine if the segments shown can form a triangle, we can apply the triangle inequality theorem. In euclidean geometry, each and every three points.

SOLVED 'The segments shown below could form a triangle. Questlon 3 of

To determine if the segments shown can form a triangle, we can apply the triangle inequality theorem. In order to form a triangle sum of the lengths of any two sides must always be greater than the length of the third side. According to the triangle inequality theorem, this is a necessary. It's one of the fundamental geometric shapes. In.

SOLVED 'The segments shown below could form a triangle. The segments

In euclidean geometry, each and every three points that are not collinear produce a distinct triangle. To determine if the segments shown can form a triangle, we can apply the triangle inequality theorem. 1 check if the sum of any two sides of the triangle is greater than the third side. According to the triangle inequality theorem, this is a.

SOLVED 'The segments shown below could form a triangle. Question 6 of

To determine if the segments shown can form a triangle, we can apply the triangle inequality theorem. In euclidean geometry, each and every three points that are not collinear produce a distinct triangle. 1 check if the sum of any two sides of the triangle is greater than the third side. It's one of the fundamental geometric shapes. In order.

The segments shown below could form a triangle. A B 1 C 8 A A. True B

1 check if the sum of any two sides of the triangle is greater than the third side. It's one of the fundamental geometric shapes. In order to form a triangle sum of the lengths of any two sides must always be greater than the length of the third side. In euclidean geometry, each and every three points that are.

Solved The segments shown below could form a triangle. 1 A. True B

According to the triangle inequality theorem, this is a necessary. It's one of the fundamental geometric shapes. In euclidean geometry, each and every three points that are not collinear produce a distinct triangle. To determine if the segments shown can form a triangle, we can apply the triangle inequality theorem. Here, 6 + 5 = 11 > 8.

SOLVED The segments shown below could form a triangle. A. True B. False

The segments shown below could form a triangle. A C 9 8 B 17 C A. True

In euclidean geometry, each and every three points that are not collinear produce a distinct triangle. In order to form a triangle sum of the lengths of any two sides must always be greater than the length of the third side. Here, 6 + 5 = 11 > 8. According to the triangle inequality theorem, this is a necessary. 1.

The segments shown below could form a triangle. 9 1 C A. True B. False

In order to form a triangle sum of the lengths of any two sides must always be greater than the length of the third side. 1 check if the sum of any two sides of the triangle is greater than the third side. In euclidean geometry, each and every three points that are not collinear produce a distinct triangle. Here,.

To Determine If The Segments Shown Can Form A Triangle, We Can Apply The Triangle Inequality Theorem.

Here, 6 + 5 = 11 > 8. According to the triangle inequality theorem, this is a necessary. It's one of the fundamental geometric shapes. In euclidean geometry, each and every three points that are not collinear produce a distinct triangle.