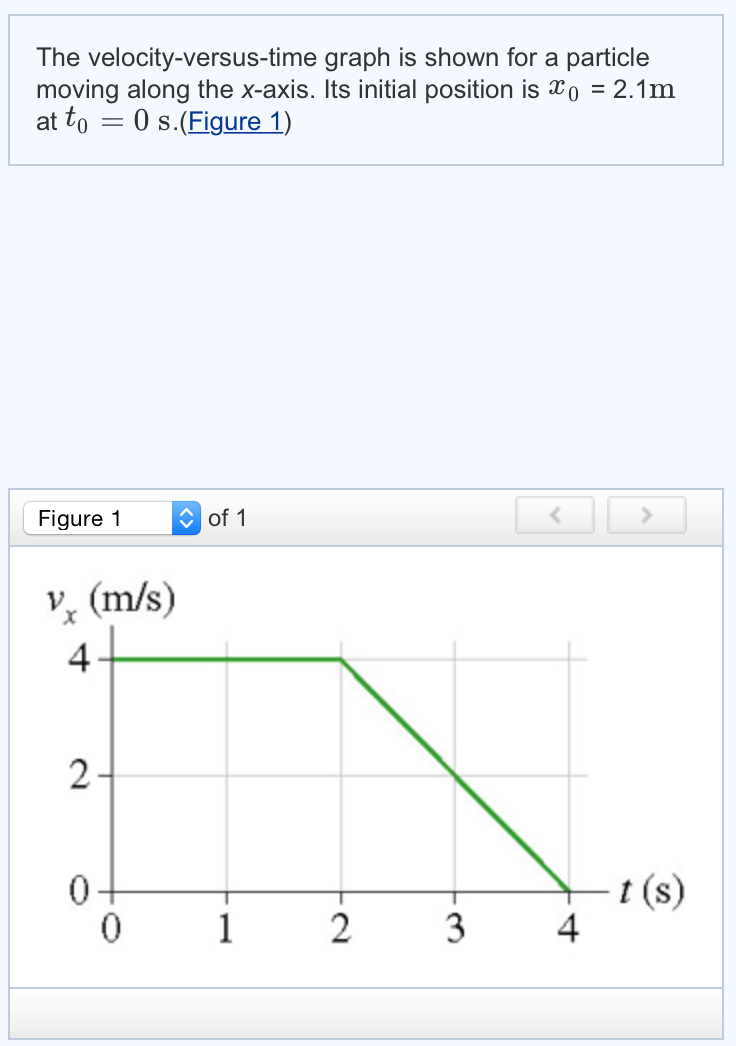
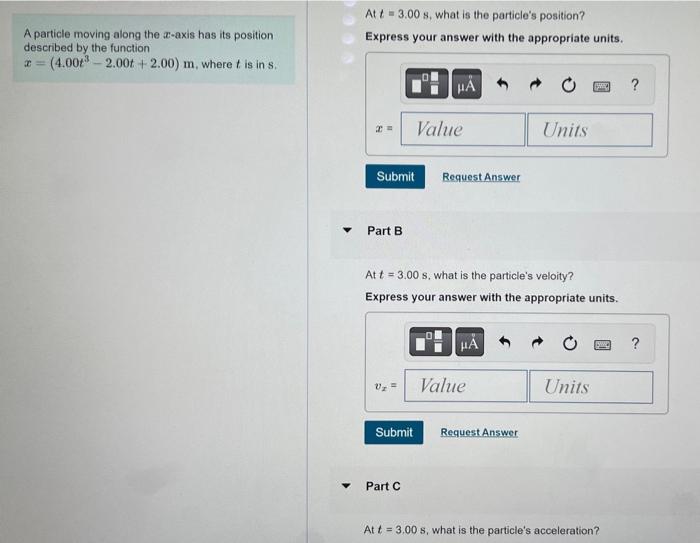
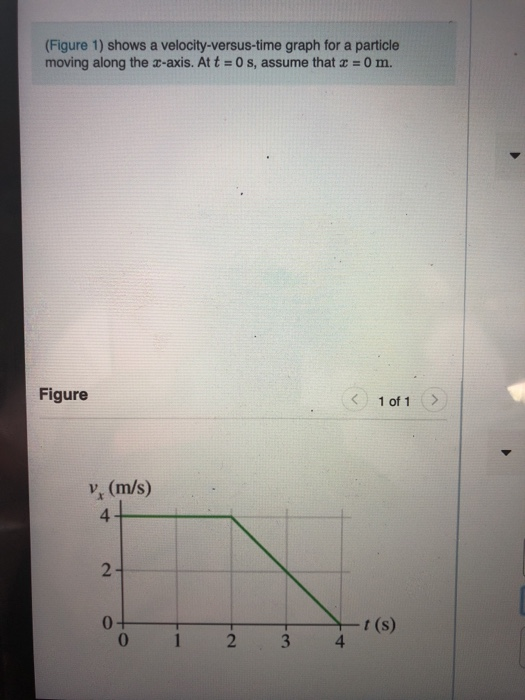
What Is The Particle S Position At T 3 0 S - We need to use the equation of motion to find the position of the particle at t = 3.0 s. If s = 0 when t = 0, determine the. In the following, motion of the particle begins at t = 0; What is the acceleration of the particle at t =. The particle does not cross the origin and the displacement between t = 3.0 s and t = 6.0 s is 16.0 meters. The initial position of the particle is given by r0 = x0i + y0j and its initial velocity is given by v0 =. The velocity of a particle traveling in a straight line is given by v = (6t 3t2) m=s, where t is in seconds. The equation of motion is: The position of a particle as it moves along the x axis is given by x = 15 e^(2t) m, wher t is in s. X = x0 + v0t + (1/2)at^2 where x is.
The particle does not cross the origin and the displacement between t = 3.0 s and t = 6.0 s is 16.0 meters. We need to use the equation of motion to find the position of the particle at t = 3.0 s. The equation of motion is: The velocity of a particle traveling in a straight line is given by v = (6t 3t2) m=s, where t is in seconds. In the following, motion of the particle begins at t = 0; The position of a particle as it moves along the x axis is given by x = 15 e^(2t) m, wher t is in s. What is the acceleration of the particle at t =. If s = 0 when t = 0, determine the. The initial position of the particle is given by r0 = x0i + y0j and its initial velocity is given by v0 =. X = x0 + v0t + (1/2)at^2 where x is.
The equation of motion is: What is the acceleration of the particle at t =. We need to use the equation of motion to find the position of the particle at t = 3.0 s. The position of a particle as it moves along the x axis is given by x = 15 e^(2t) m, wher t is in s. The velocity of a particle traveling in a straight line is given by v = (6t 3t2) m=s, where t is in seconds. In the following, motion of the particle begins at t = 0; If s = 0 when t = 0, determine the. The initial position of the particle is given by r0 = x0i + y0j and its initial velocity is given by v0 =. The particle does not cross the origin and the displacement between t = 3.0 s and t = 6.0 s is 16.0 meters. X = x0 + v0t + (1/2)at^2 where x is.
(Solved) Part A What is the particle's position at t =1.0s ? Express
The position of a particle as it moves along the x axis is given by x = 15 e^(2t) m, wher t is in s. The particle does not cross the origin and the displacement between t = 3.0 s and t = 6.0 s is 16.0 meters. The initial position of the particle is given by r0 = x0i.
Solved A particle's position as a function of time is given
The velocity of a particle traveling in a straight line is given by v = (6t 3t2) m=s, where t is in seconds. The equation of motion is: The particle does not cross the origin and the displacement between t = 3.0 s and t = 6.0 s is 16.0 meters. X = x0 + v0t + (1/2)at^2 where x.
Solved A particle moves along the xaxis so that its
If s = 0 when t = 0, determine the. The initial position of the particle is given by r0 = x0i + y0j and its initial velocity is given by v0 =. The velocity of a particle traveling in a straight line is given by v = (6t 3t2) m=s, where t is in seconds. In the following, motion.
Solved A particle's position is given by x=3t−t3 Find the
The particle does not cross the origin and the displacement between t = 3.0 s and t = 6.0 s is 16.0 meters. We need to use the equation of motion to find the position of the particle at t = 3.0 s. X = x0 + v0t + (1/2)at^2 where x is. The velocity of a particle traveling in.
Solved At t=3.00 s, what is the particle's position? A
The equation of motion is: The position of a particle as it moves along the x axis is given by x = 15 e^(2t) m, wher t is in s. If s = 0 when t = 0, determine the. The velocity of a particle traveling in a straight line is given by v = (6t 3t2) m=s, where t.
Solved what is the particle’s position at t=3 seconds? what
We need to use the equation of motion to find the position of the particle at t = 3.0 s. The velocity of a particle traveling in a straight line is given by v = (6t 3t2) m=s, where t is in seconds. If s = 0 when t = 0, determine the. The equation of motion is: X =.
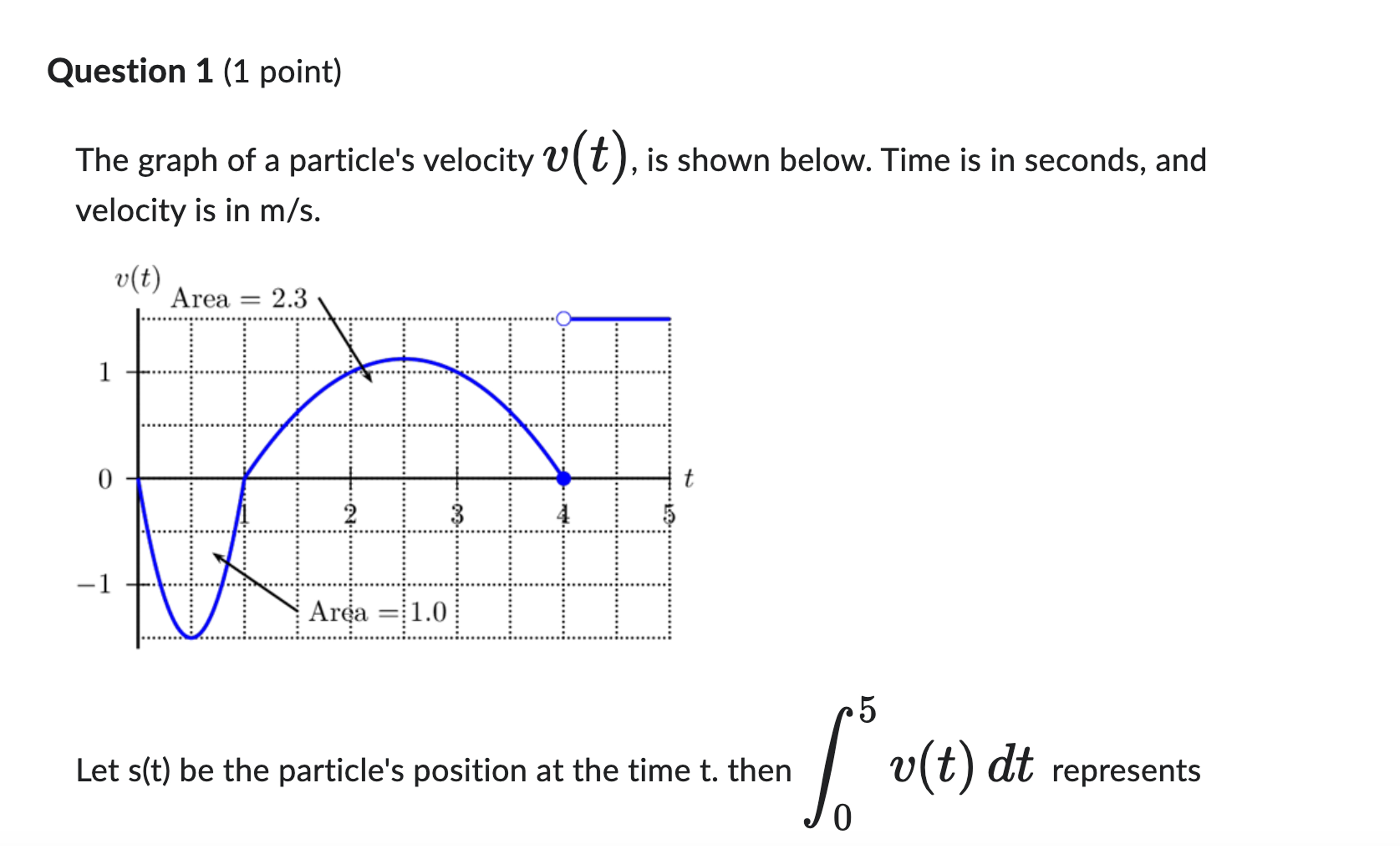
Solved Let s(t) be the particle's position at the time t.
The initial position of the particle is given by r0 = x0i + y0j and its initial velocity is given by v0 =. The velocity of a particle traveling in a straight line is given by v = (6t 3t2) m=s, where t is in seconds. The particle does not cross the origin and the displacement between t = 3.0.
Solved Let's say a particle's position, as a function of
If s = 0 when t = 0, determine the. The equation of motion is: What is the acceleration of the particle at t =. The velocity of a particle traveling in a straight line is given by v = (6t 3t2) m=s, where t is in seconds. In the following, motion of the particle begins at t = 0;
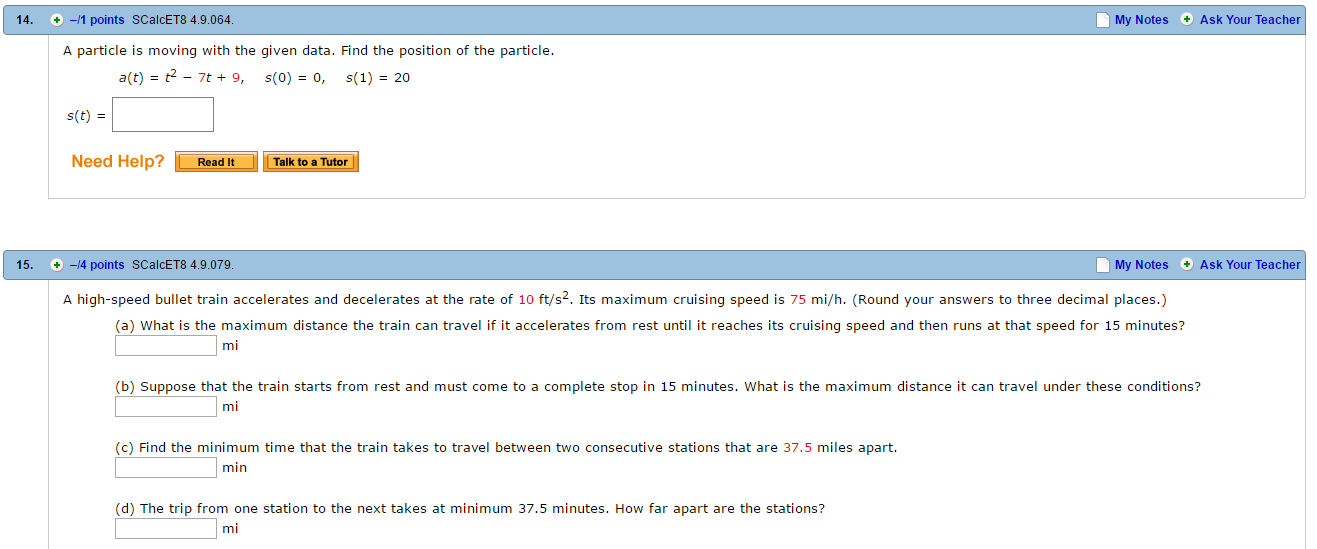
Solved A particle is moving with the given data. Find the
In the following, motion of the particle begins at t = 0; The position of a particle as it moves along the x axis is given by x = 15 e^(2t) m, wher t is in s. The initial position of the particle is given by r0 = x0i + y0j and its initial velocity is given by v0 =..
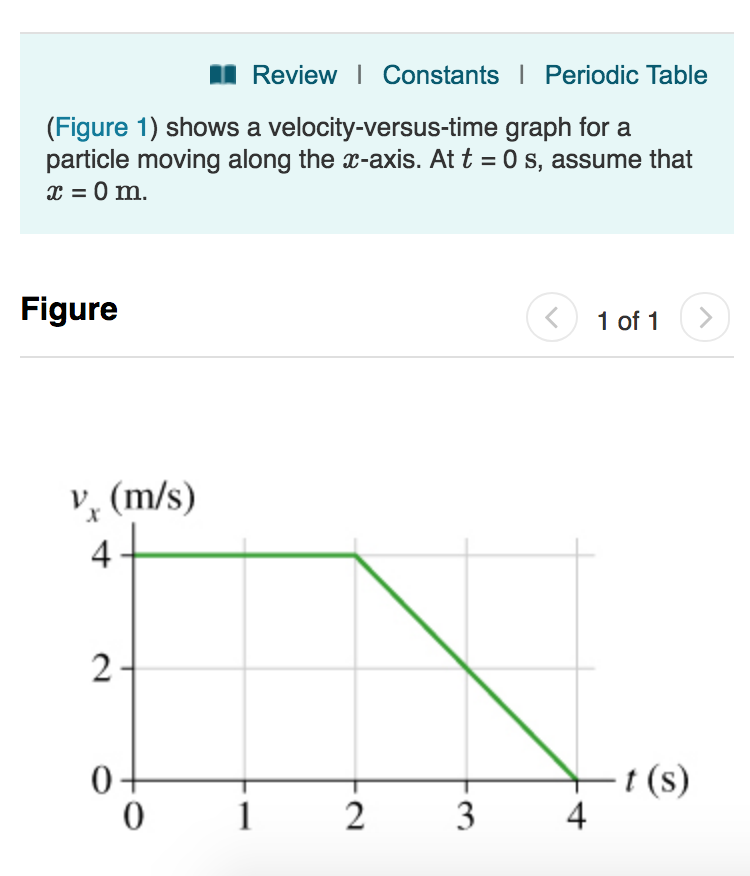
Solved a. What is the particle's position at t = 1.0 s? b.
The particle does not cross the origin and the displacement between t = 3.0 s and t = 6.0 s is 16.0 meters. X = x0 + v0t + (1/2)at^2 where x is. The velocity of a particle traveling in a straight line is given by v = (6t 3t2) m=s, where t is in seconds. What is the acceleration.
If S = 0 When T = 0, Determine The.
The velocity of a particle traveling in a straight line is given by v = (6t 3t2) m=s, where t is in seconds. In the following, motion of the particle begins at t = 0; The equation of motion is: The initial position of the particle is given by r0 = x0i + y0j and its initial velocity is given by v0 =.
The Position Of A Particle As It Moves Along The X Axis Is Given By X = 15 E^(2T) M, Wher T Is In S.
The particle does not cross the origin and the displacement between t = 3.0 s and t = 6.0 s is 16.0 meters. What is the acceleration of the particle at t =. X = x0 + v0t + (1/2)at^2 where x is. We need to use the equation of motion to find the position of the particle at t = 3.0 s.