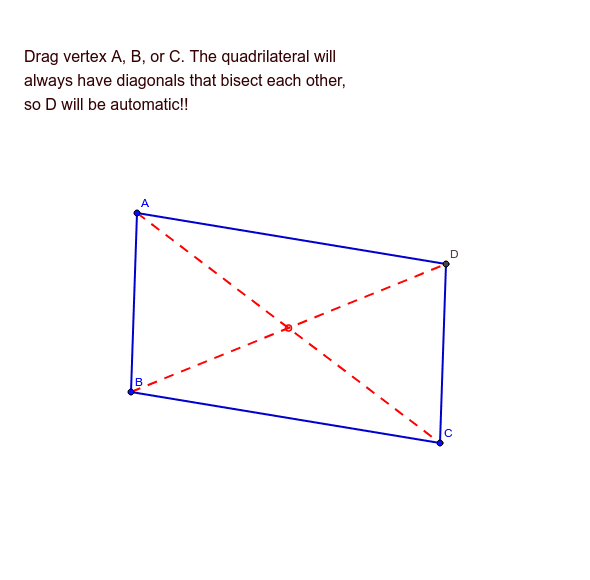
What Quadrilateral Has Diagonals That Bisect Each Other - Also known as mutually bisecting diagonals, they divide each other into half after they meet. Parallelograms, rectangles, rhombi, and squares are examples of quadrilaterals that always have both diagonals bisecting each other. On the other hand, kites have only one diagonal that bisects. Another interesting thing is that the diagonals (dashed lines) meet in the middle at a right angle. In other words they bisect (cut in half) each other at right angles. Let us take the example of a square. In conclusion, all of the listed quadrilaterals have diagonals that bisect each other: Therefore, the answer is that. Theorem 8.7 if the diagonals of a quadrilateral bisect each other, then it is a parallelogram. Abcd is a quadrilateral with ac and bd are diagonals intersecting at o.
In conclusion, all of the listed quadrilaterals have diagonals that bisect each other: Abcd is a quadrilateral with ac and bd are diagonals intersecting at o. 1) diagonals that bisect each other: Parallelograms, rectangles, rhombi, and squares are examples of quadrilaterals that always have both diagonals bisecting each other. Another interesting thing is that the diagonals (dashed lines) meet in the middle at a right angle. Theorem 8.7 if the diagonals of a quadrilateral bisect each other, then it is a parallelogram. Let us take the example of a square. On the other hand, kites have only one diagonal that bisects. Therefore, the answer is that. Also known as mutually bisecting diagonals, they divide each other into half after they meet.
Abcd is a quadrilateral with ac and bd are diagonals intersecting at o. Also known as mutually bisecting diagonals, they divide each other into half after they meet. Parallelograms, rectangles, rhombi, and squares are examples of quadrilaterals that always have both diagonals bisecting each other. On the other hand, kites have only one diagonal that bisects. Let us take the example of a square. 1) diagonals that bisect each other: In other words they bisect (cut in half) each other at right angles. Another interesting thing is that the diagonals (dashed lines) meet in the middle at a right angle. Theorem 8.7 if the diagonals of a quadrilateral bisect each other, then it is a parallelogram. Therefore, the answer is that.
Name the quadrilateral whose diagonals are equal and bisect each other
Also known as mutually bisecting diagonals, they divide each other into half after they meet. Let us take the example of a square. Therefore, the answer is that. 1) diagonals that bisect each other: In conclusion, all of the listed quadrilaterals have diagonals that bisect each other:
If the diagonals of a quadrilateral bisect each other... GeoGebra
Let us take the example of a square. Parallelograms, rectangles, rhombi, and squares are examples of quadrilaterals that always have both diagonals bisecting each other. Theorem 8.7 if the diagonals of a quadrilateral bisect each other, then it is a parallelogram. Abcd is a quadrilateral with ac and bd are diagonals intersecting at o. On the other hand, kites have.
Ex 8.1, 3 Show that if diagonals of a quadrilateral bisect
In other words they bisect (cut in half) each other at right angles. On the other hand, kites have only one diagonal that bisects. Also known as mutually bisecting diagonals, they divide each other into half after they meet. Abcd is a quadrilateral with ac and bd are diagonals intersecting at o. In conclusion, all of the listed quadrilaterals have.
If the diagonals of a quadrilateral are equal and bisect each other at
Theorem 8.7 if the diagonals of a quadrilateral bisect each other, then it is a parallelogram. In other words they bisect (cut in half) each other at right angles. Parallelograms, rectangles, rhombi, and squares are examples of quadrilaterals that always have both diagonals bisecting each other. Let us take the example of a square. Another interesting thing is that the.
Name the quadrilateral whose diagonals are equal and bisect each other
On the other hand, kites have only one diagonal that bisects. In conclusion, all of the listed quadrilaterals have diagonals that bisect each other: Abcd is a quadrilateral with ac and bd are diagonals intersecting at o. In other words they bisect (cut in half) each other at right angles. Therefore, the answer is that.
Show that if the diagonals of a quadrilateral are equal and bisect each
Theorem 8.7 if the diagonals of a quadrilateral bisect each other, then it is a parallelogram. Also known as mutually bisecting diagonals, they divide each other into half after they meet. Another interesting thing is that the diagonals (dashed lines) meet in the middle at a right angle. Let us take the example of a square. Parallelograms, rectangles, rhombi, and.
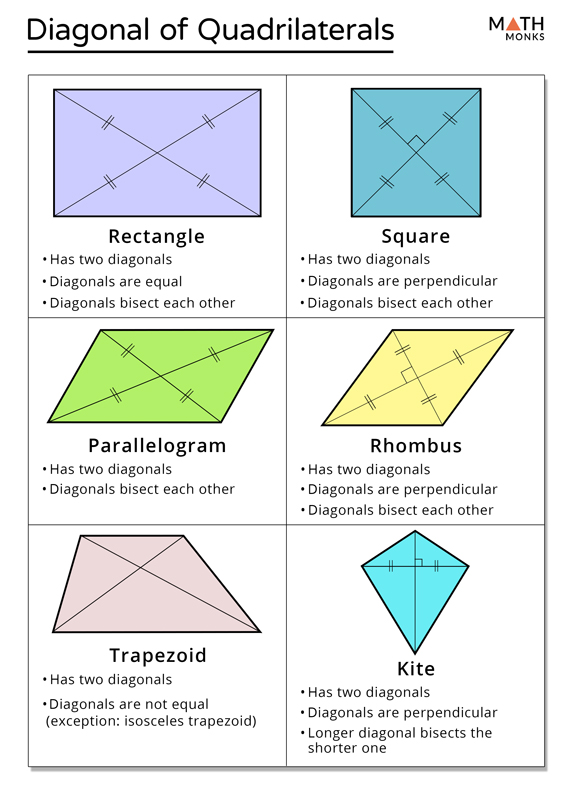
Diagonal of Quadrilateral
Theorem 8.7 if the diagonals of a quadrilateral bisect each other, then it is a parallelogram. In conclusion, all of the listed quadrilaterals have diagonals that bisect each other: On the other hand, kites have only one diagonal that bisects. 1) diagonals that bisect each other: In other words they bisect (cut in half) each other at right angles.
Theorem 8.6 Class 9 Diagonals of a parallelogram bisect each other
Another interesting thing is that the diagonals (dashed lines) meet in the middle at a right angle. Therefore, the answer is that. Also known as mutually bisecting diagonals, they divide each other into half after they meet. In other words they bisect (cut in half) each other at right angles. Theorem 8.7 if the diagonals of a quadrilateral bisect each.
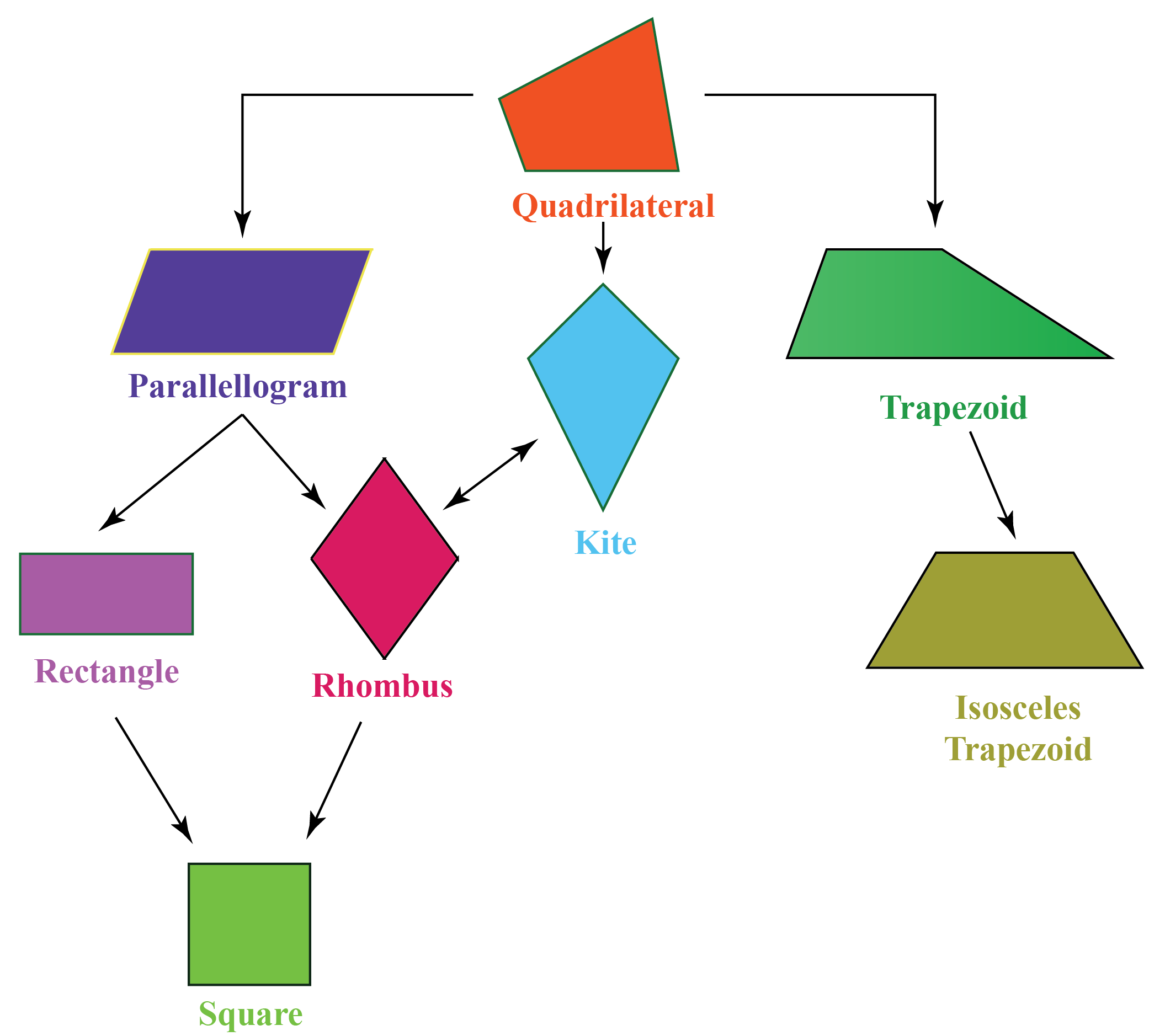
Quadrilaterals Types Properties What is Quadrilaterals
Another interesting thing is that the diagonals (dashed lines) meet in the middle at a right angle. In other words they bisect (cut in half) each other at right angles. Let us take the example of a square. Abcd is a quadrilateral with ac and bd are diagonals intersecting at o. 1) diagonals that bisect each other:
Quadrilateral where both diagonals bisect each other is a Parallelogram
Theorem 8.7 if the diagonals of a quadrilateral bisect each other, then it is a parallelogram. Another interesting thing is that the diagonals (dashed lines) meet in the middle at a right angle. Let us take the example of a square. Therefore, the answer is that. 1) diagonals that bisect each other:
Abcd Is A Quadrilateral With Ac And Bd Are Diagonals Intersecting At O.
Therefore, the answer is that. Also known as mutually bisecting diagonals, they divide each other into half after they meet. 1) diagonals that bisect each other: Theorem 8.7 if the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
Parallelograms, Rectangles, Rhombi, And Squares Are Examples Of Quadrilaterals That Always Have Both Diagonals Bisecting Each Other.
On the other hand, kites have only one diagonal that bisects. Another interesting thing is that the diagonals (dashed lines) meet in the middle at a right angle. In conclusion, all of the listed quadrilaterals have diagonals that bisect each other: In other words they bisect (cut in half) each other at right angles.